轨道角动量涡旋光金属超表面设计（二）

GMPT, 2025/12/04

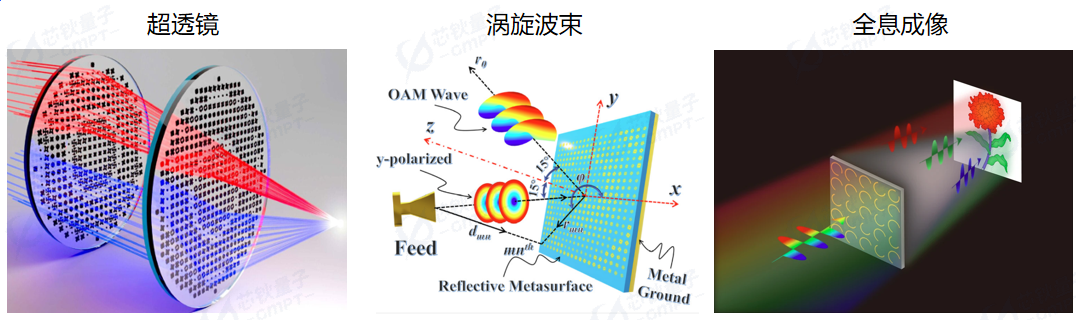
  在上一篇文章《轨道角动量涡旋光金属超表面设计（一）》中，我们主要介绍了如何对可调控电磁波波前相位的金属超原子进行仿真，建立超原子库以满足后续超表面设计的需求。本文将进一步介绍如何利用之前得到的超原子库来设计我们所需的超表面的应用，即最终达到生成轨道角动量涡旋光的目标。根据这种方法论，我们可以设计出多种多样的超表面应用，超表面的具体调控波前相位的应用如图1所示。目前，超表面可以用来生成超透镜，产生涡旋光以及全息成像等等一系列应用。

图1. 不同超表面功能示意图

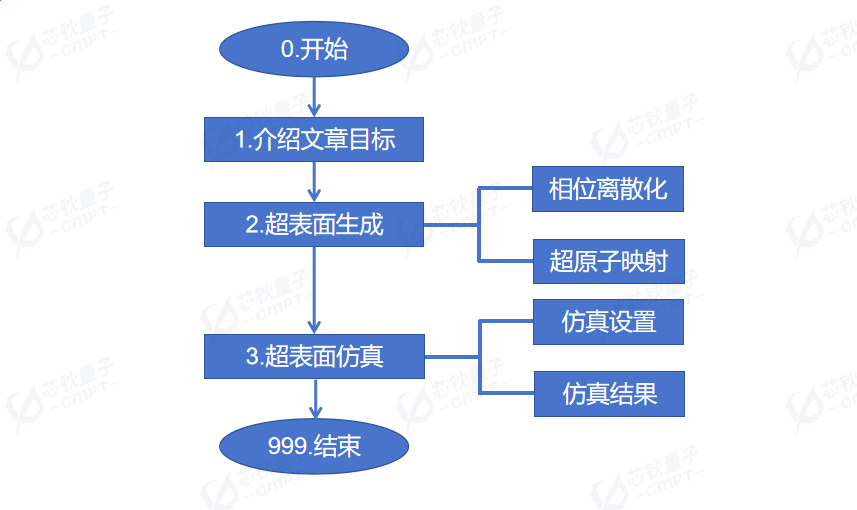
  本文的文章结构如图2所示。本文在Macondo软件的FDTD3D求解器中，对可调控电磁波幅度和相位的金属超表面进行仿真，目标是基于该结构生成我们所需的一阶涡旋光束。本文首先介绍了如何通过相位离散化的方式将之前设计的超原子映射到一个二维分布中，从而生成超表面。之后我们在Macondo软件中对超表面进行建模以及FDTD3D求解器仿真，得到一阶轨道角动量涡旋光，并且对生成的涡旋光质量进行评估。

图2. 文章结构

一、超表面生成

1.1 轨道角动量相位离散化

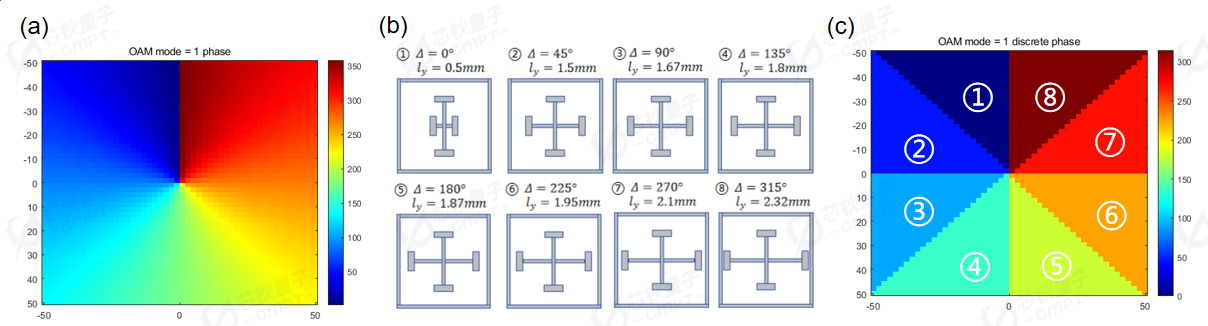
  在《轨道角动量涡旋光金属超表面设计（一）》中，我们谈到了一阶轨道角动量涡旋波束的理想相位分布，其分布如图3(a)所示，之后我们需要将该理想相位分布离散化。如图3(b)所示，我们之前设计的超原子的相位为间隔45°，范围0°到360°的离散值。如图3(c)所示，我们将轨道角动量涡旋波束的相位分布离散到一个50 $\times \backslash times$ 50 的矩形网格中，相位的离散值为0°到360°的45°等间隔相位，从而与图3(b)中的超原子的相位差值所匹配。

图3. 轨道角动量离散相位图

1.2 超原子长度映射

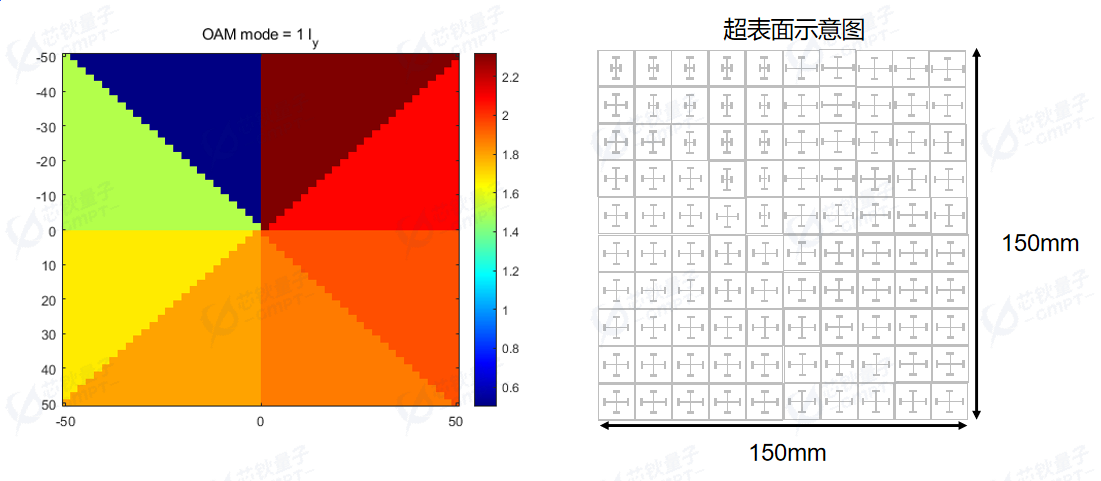
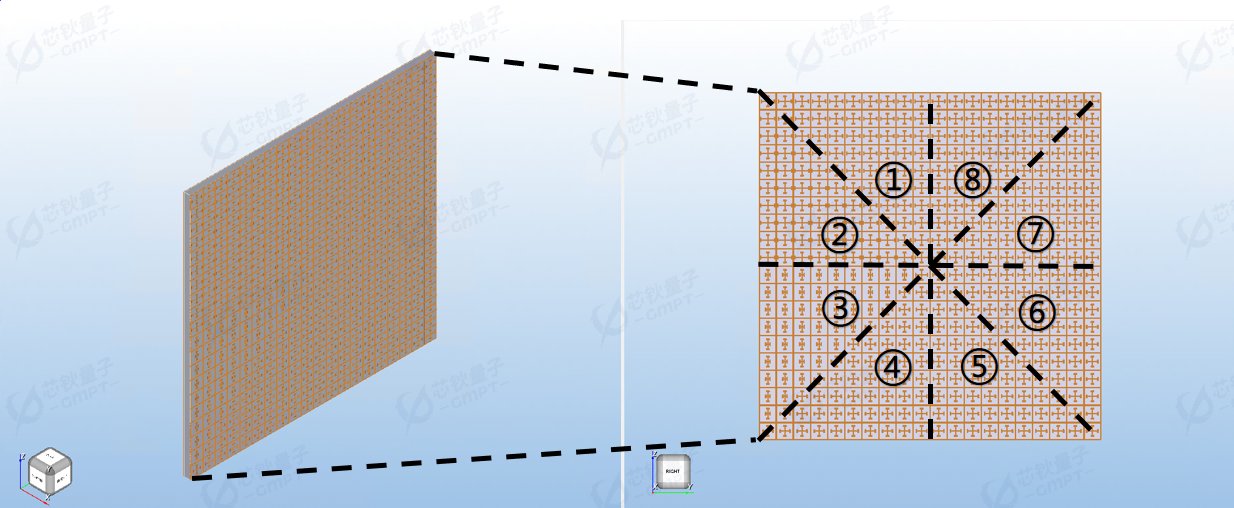
  如图4(a)所示，在得到离散化之后的轨道角动量后，我们将之前所得到的超原子臂长 $l_{y}l\_y$ 与其对应的相位一一映射，得到我们所需要的超表面中每个超原子所对应的臂长 $l_{y}l\_y$， 然后将其填充进超表面中，得到我们所需的超表面模型。超表面示意图如图4(b)所示，示意图大小为10 $\times \backslash times$ 10 个单元，实际建模大小为50 $\times \backslash times$ 50 个单元。

图4. 超原子臂长分布与超表面模型

二、超表面仿真与讨论

2.1 超表面仿真设置

   超表面仿真设置图如图5所示：

• 工作频率: 本文中超表面的工作频率为25GHz。
  
• 激励源: 本文中激励源设置为y极化平面波（电场沿y方向），沿x负方向入射，使用TFSF激励源。
  
• 边界条件: 由于超表面的仿真是在自由空间内，所以x，y，z方向边界条件均为PML（完全匹配层），仿真自由空间的边界条件。
  
• 网格设置：由于计算资源的限制，求解器网格设置为每个波长内有4个网格单元。
  
• 仿真范围：FDTD求解器的范围为x方向长度50mm，y和z方向150mm。
  
• 仿真结果：通过监控器监测不同平面超表面的近场反射相位图，监测器距离超表面100mm。
  

图5. 超表面仿真设置

2.2 超表面仿真结果

  一阶轨道角动量涡旋光电场理论公式为：
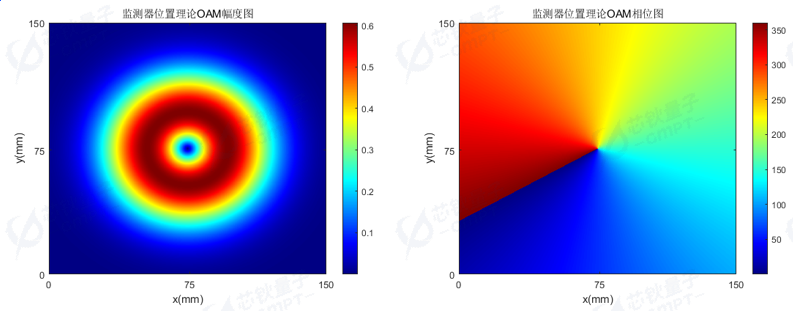
$$E(r,\varphi ,z)=E_0(\frac{\sqrt{2}r}{w(z)})e^{-\frac{r^2}{w(z{)}^2}}{e}^{-ikz+i\varphi }E(r,\backslash phi,z)=\; E\_\{0\}(\backslash frac\{\backslash sqrt\{2\}r\}\{w(z)\})e^\{-\backslash frac\{r^\{2\}\}\{w(z)^\{2\}\}\}e^\{-ikz+i\backslash phi\}$$   其中$w(z)=\sqrt{1+(\frac{z}{z_R}{)}^2}w(z)\; =\; \backslash sqrt\{1+(\backslash frac\{z\}\{z\_\{R\}\})^\{2\}\}$是光束半径，随传播距离变化。 $z_R=\frac{\pi }{\lambda }z\_\{R\}\; =\; \backslash frac\{\backslash pi\}\{\backslash lambda\}$ 是瑞利范围。根据这个公式，我们可以画出$z=100mmz=100mm$时OAM波束的理论电场图案。如图6所示，理论轨道角动量波束呈现甜甜圈型的幅度分布以及涡旋状的相位分布。在超原子设计中，我们使幅度均匀为1是为了简化超表面设计、降低制造难度，并确保相位调制在生成OAM波中起主导作用[2]。

图6. 轨道角动量波束理论电场图案

  超表面仿真得到的涡旋光幅度和相位图如图7（a）-（b）所示，此时监视器位置距离超表面45mm。图7（a）能够观察到甜甜圈型的幅度分布,即幅度图中心的幅度为0，中心周围幅度较大。图7（b）能够观察到涡旋状的相位分布。
  对于轨道角动量波束来说，评估其生成质量的一个重要参数为模式纯度（mode purity），其代表不同涡旋光模式在总光场功率中所占的比例，其表达式为：
$$\mathbf{M}\mathbf{P}=\frac{{\int }_0^{\mathrm{\infty }}\mathrm{\mid }{a}_l(r){\mathrm{\mid }}^{2}rdr}{{\int }_0^{\mathrm{\infty }}{\int }_0^{2\pi }\mathrm{\mid }\phi (r,\varphi ){\mathrm{\mid }}^{2}rdrd\varphi }\backslash mathbf\{MP\}=\; \backslash frac\{\backslash int\_\{0\}^\{\backslash infty\}\; |a\_\{l\}(r)|^2\; r\; dr\}\{\backslash int\_\{0\}^\{\backslash infty\}\; \backslash int\_\{0\}^\{2\backslash pi\}\; |\backslash varphi(r,\backslash phi)|^2\; rdrd\backslash phi\}$$   其中$\phi (r,\varphi )\backslash varphi(r,\backslash phi)$ 是仿真或实验测得的涡旋光的复振幅分布，$a_l(r)=\frac{1}{2\pi }{\int }_0^{2\pi }\phi (r,\varphi )e^{-il\varphi }d\varphi a\_\{l\}(r)\; =\; \backslash frac\{1\}\{2\backslash pi\}\; \backslash int\_\{0\}^\{2\backslash pi\}\; \backslash varphi(r,\backslash phi)\; e^\{-il\backslash phi\}d\backslash phi$ 是角向傅里叶系数，分母表示光场的总功率，分子表示模式$ll$的功率。
  超表面的模式纯度图如图7（c）所示，可以看到此时生成的主模式为$l=1l=1$，与之前仿真的设计相符，主模式纯度为0.731。

图7. 超表面仿真结果与模式纯度

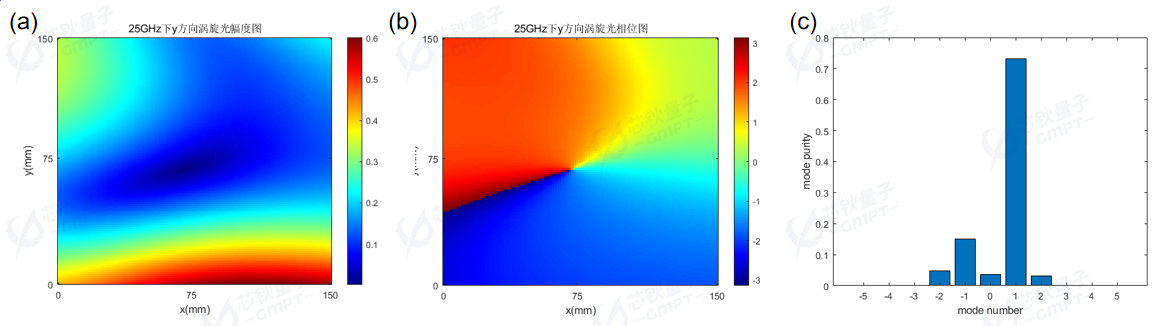
  提高涡旋光模式纯度的方法有加密网格，可以使得计算更精确；或者是增加超表面中超原子的个数，使得离散化更为精细；或者是加大仿真的区域，使得涡旋光更完整的传播。

2.3 超表面仿真总结

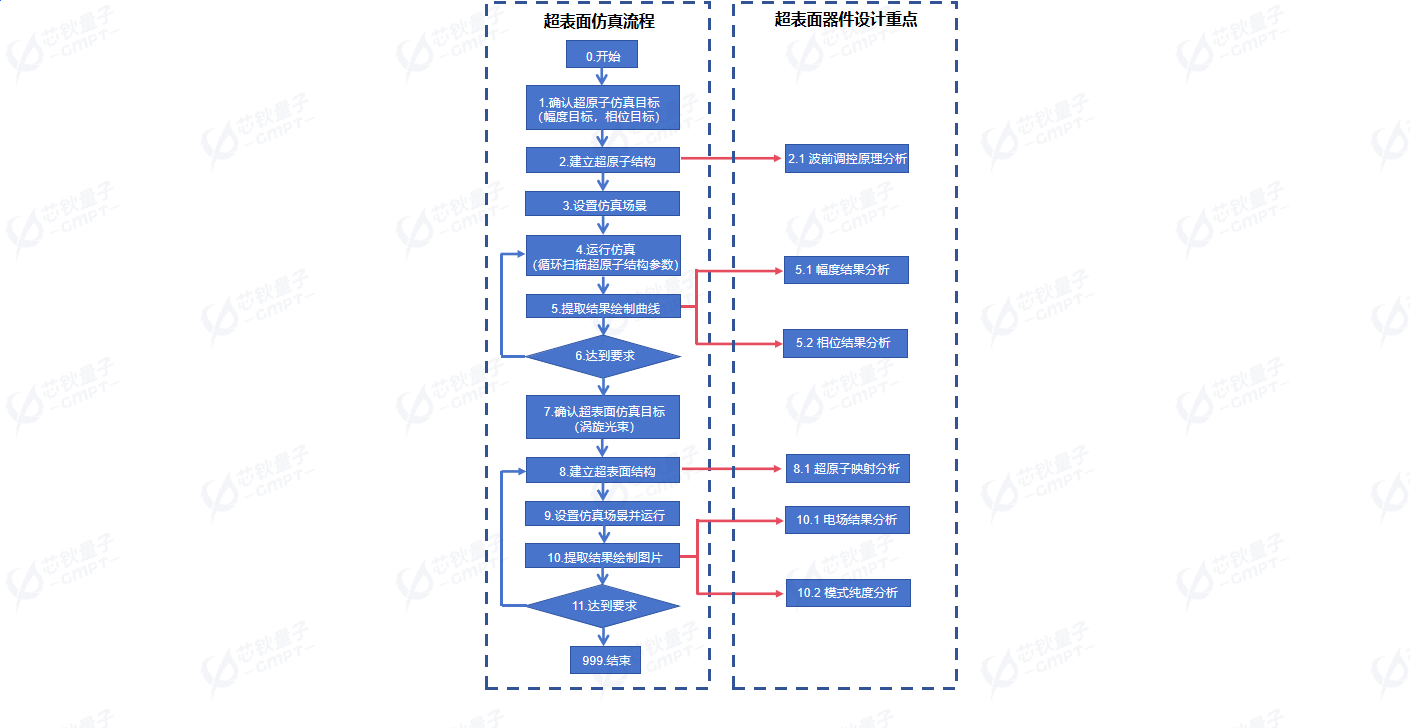
  在完成了超表面的仿真后，如图8所示，我们可以总结得到超表面的完整仿真流程以及在仿真流程中所需要关注的设计重点。在超原子设计过程中，我们的设计重点是超原子波前相位的调控原理以及仿真得到的S参数的幅度和相位；在超表面设计过程中，我们的设计重点是超原子的映射方式以及仿真得到的超表面电场分布以及模式纯度。

图8. 超表面仿真流程以及设计重点

三、总结

  本文完成了金属超表面生成涡旋光的结果验证阶段，在Macondo FDTD3D求解器中利用平面光入射到超表面上生成了轨道角动量涡旋光，并且对生成的光束质量进行了评估，从而在Macondo中实现了一个完整的金属超表面设计流程。

参考

[1] L. Shao, Z. Li, et al. Multi-Channel Metasurface for Versatile Wavefront and Polarization Manipulation[J]. Advanced Materials Technologies, 2022.
[2] X. Xu, C. Wu, et al. Generating an orbital-angular-momentum beam with a metasurface of gradient reflective phase[J]. Optical Materials Express, 2016.