求解器

Macondo软件提供了多个求解器选项，包括FDTD3D求解器、EME3D求解器和FDE求解器。用户可以根据仿真需求和特点选择适用的解决方案。

FDTD3D求解器

FDTD3D求解器采用时域有限差分算法，用于严格求解全矢量Maxwell方程组。麦克斯韦旋度方程：

\nabla \times \textbf{H} = \frac{\partial \textbf{D}}{\partial t} + \textbf{J}

\nabla \times \textbf{E} = -\frac{\partial \textbf{B}}{\partial t} - \textbf{J}_m

时域有限差分迭代方程：

E^{n+1}_x(i+\frac{1}{2},j,k) = C_1\cdot E^{n+1}_{x}(i+\frac{1}{2},j,k)

+C_2\cdot \left[H^{n+\frac{1}{2}}_{z}(i+\frac{1}{2},j+\frac{1}{2},k)-H^{n+\frac{1}{2}}_{z}(i+\frac{1}{2},j-\frac{1}{2},k)\right]

-C_3\cdot \left[H^{n+\frac{1}{2}}_{y}(i+\frac{1}{2},j,k+\frac{1}{2})-H^{n+\frac{1}{2}}_{y}(i+\frac{1}{2},j,k-\frac{1}{2})\right] ,

C_1 = \frac{2\varepsilon-\sigma\Delta t}{2\varepsilon+\sigma\Delta t}, C_2 = \frac{2\Delta t}{(2\varepsilon+\sigma\Delta t)\cdot\Delta y}, C_3 = \frac{2\Delta t}{(2\varepsilon+\sigma\Delta t)\cdot\Delta z},

基于时空关系的Yee网格离散化，通过迭代交替推演每个时间步长和空间步长的电磁特性，并注入脉冲激励，使一次仿真可以获得光源带宽响应。这是研究波动光学和电磁波问题的主要技术手段。

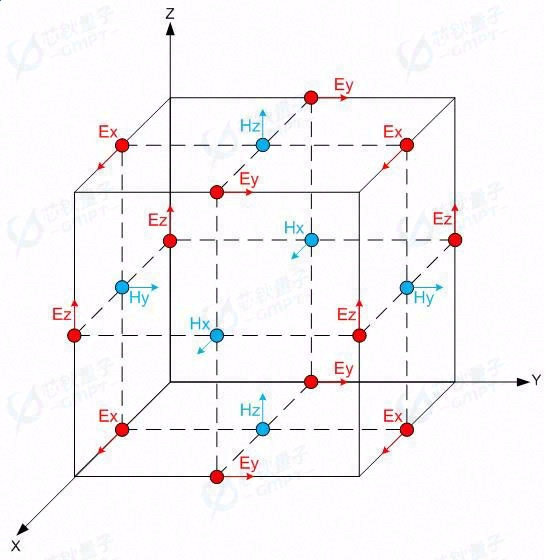
Yee Cell 网格：

光波导中模式传播演化过程：

EME3D求解器是基于模式展开算法和模式传播算法，用于分析和优化光波导器件和结构。

将仿真区域在x方向分成多个yz平面的切片，计算每个切片的模式和交叠积分，通过模式传播算法和模式展开算法获得切片和端口的S参数。计算速度和计算精度主要取决于端口和切面的计算模式的数量。

FDE求解器是基于有限差分本征模式求解算法，用户分析波导模式分布、有效折射率、模场偏振态和波导损耗。

基于有限差分的结构化离散网格和折射率共形算法，可以快速求解空间截面的模式分布和有效折射率。

FDE求解器：专用于波导2D模式计算设计的仿真器。其中，FDE Analysis分析功能，可以快速扫描不同频率的模式，结合NP Density Import 功能，能够求解由折射率扰动带来电光响应特性。

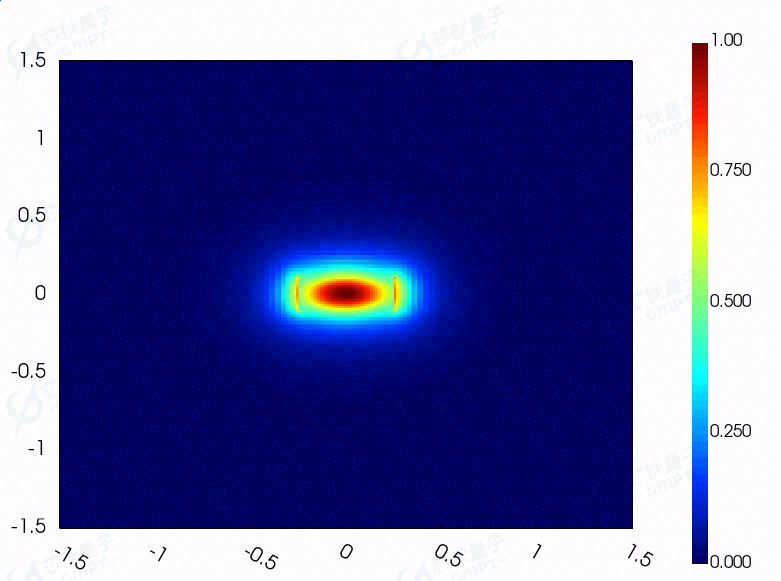
模式场分布：

（a）直波导基模电场分量/磁场分量

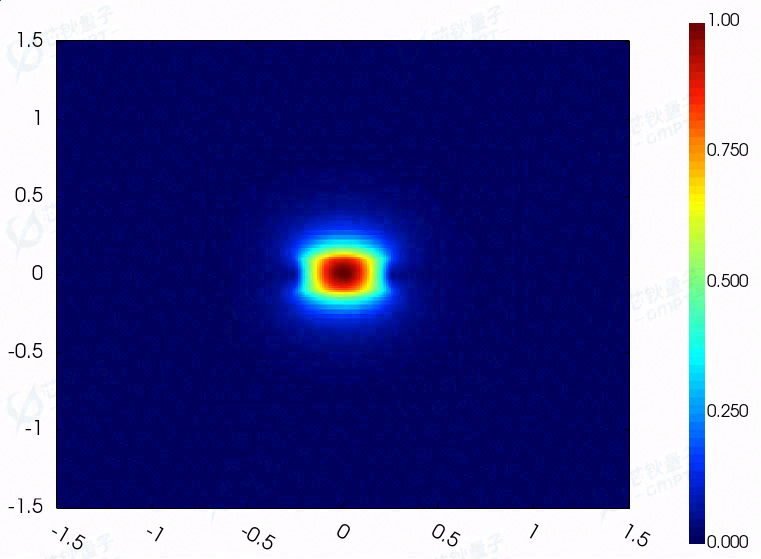
（b）脊波导基模电场分量/磁场分量

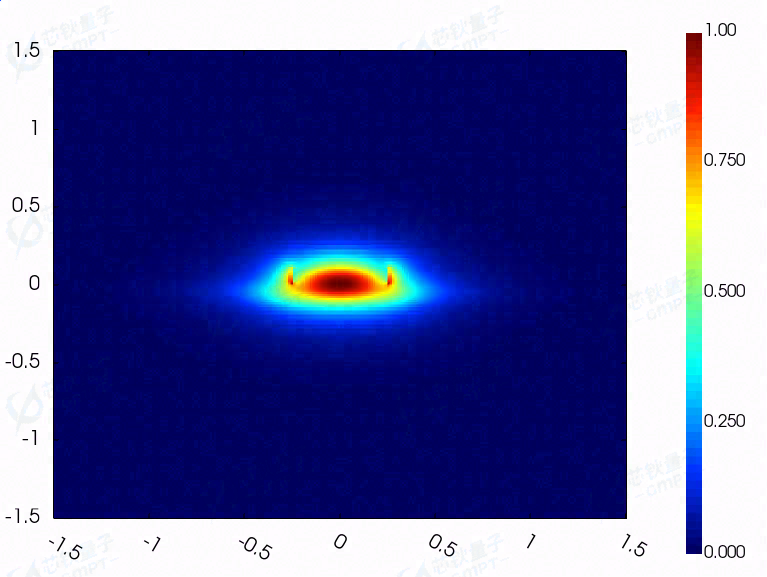
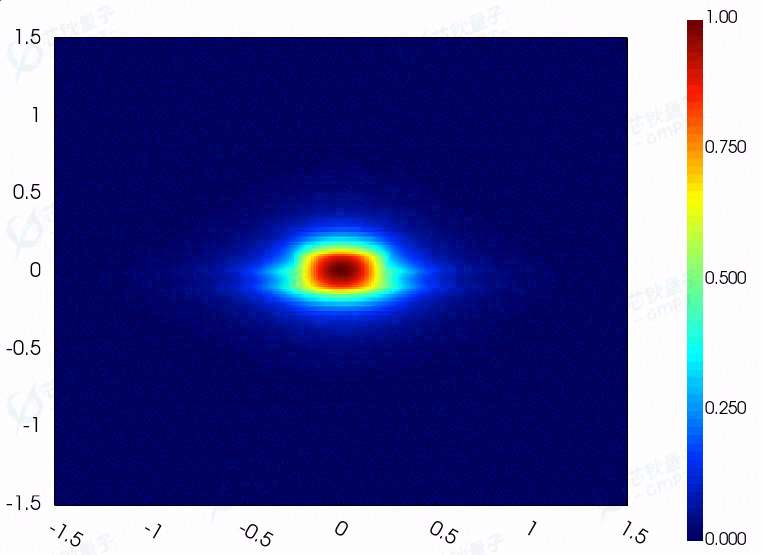
共形网格和网格划分技术是保证时域有限差分算法计算准确的基础条件。

共形网格主要解决在材料折射率发生突变的情况下的计算误差，可以在使用较少计算资源的情况下获得精确而稳定的结果。

软件处理场景中材料折射率突变网格的方法有：

Advanced Confromal 方法：通过物理方程推导，综合各类共形处理方法的优势，经过严格调校，解决了渐变过渡网格不同介质材料交界面计算数值误差大的问题。
Confromal 方法：体积加权平均法，虽然缺乏严格物理基础，但简单准确，适用于大部分场景。
StairCase 方法：传统的阶梯型折射率网格，简单快速，但存在较大数值误差。

软件处理场景和几何的网格划分方法有：

共形网格划分直波导与弯曲波导：

在求解区域边界处，通过边界条件来表征不同的实际空间特征，软件内置边界条件包括：

Metal：全反射的边界条件，电磁波能量会被限制在仿真区域内，常被作为模式计算的边界条件。
PML：吸收边界条件，以多层变化尺度的介质层作为匹配吸收层，抑制光场能量的反射，从而实现入射光的吸收，是FDTD常用的模拟无限大仿真区域或不考虑反射影响的边界条件。
Bloch：周期边界条件，主要应用于无限大平面波斜入射的情况，可以解决平面波光源在边界处相位不连续的问题。

为了提高仿真效率，软件内置求解计算设置：

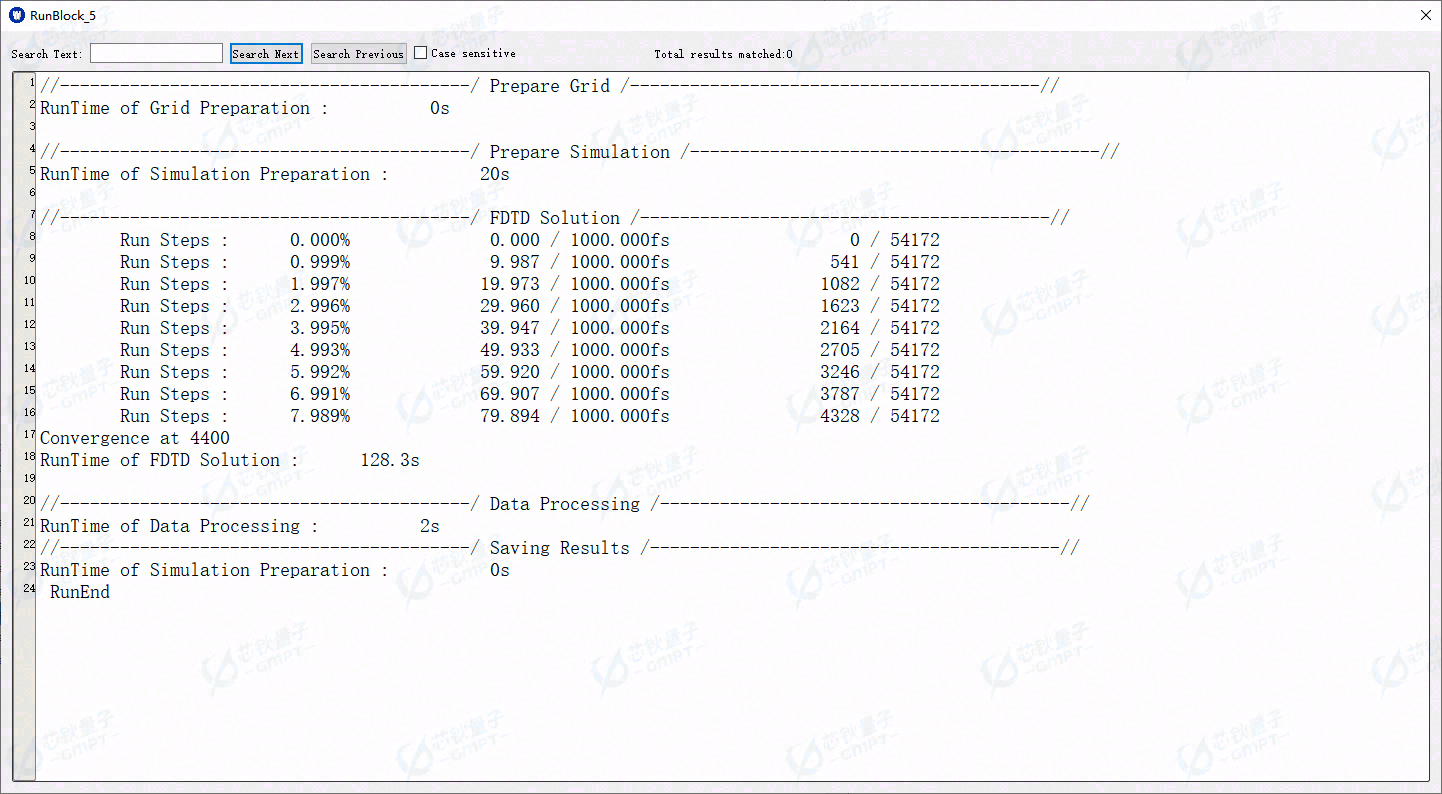
FDTD迭代提前收敛，运行记录Log：