Henyey-Greenstein 体散射

GMPT

1 应用背景

  Henyey-Greenstein 是适用于描述光进入材料发生散射的一种最为简易和普遍的情况，通常应用于大气科学，生命科学的仿真案例中。Henyey-Greenstein 散射并非是基于电磁学原理，而是基于经验的一种模型，是由 Henyey 和 Greenstein 在 1941 年提出。由于是经验性的模型，HG相函数的优点在于其简单性和灵活性，能够模拟各种不同的散射特性，是一个十分有用的工具，可以帮助科学家和工程师更好地理解和模拟光线与材料的交互过程。

2 原理介绍

  体散射一个重要的参数是平均自由程 (Mean Free Path, MFP)，其物理意义是光在物体中行进而不发生散射的距离的期望值。
  平均自由程的倒数，也就是散射系数 (Scattering Coefficient)，其物理意义为单位距离发生次数的期望值。
  我们通常将 MFP 的默认值设为无限大。MFP 缩放系数（MFP Scaled Factor）是对 MFP 进行缩放的系数。通常应用在粒子浓度发生变化的情境，和粒子浓度的倒数成正相关。（粒子浓度和平均自由程成反比）
  缩放的 MFP 和原 MFP 的关系为：

$$ScaledMFP=MFP\ast MFPScaledFactor\{Scaled~MFP\; =\; MFP\; *\; MFP~Scaled~Factor\}$$

  散射过程是泊松过程，泊松过程的意思是在每一点散射的几率是大体相同的，泊松分布的 PDF 为

$$p(\mu )=\frac{1}{2}\frac{1-g^2}{{[1+g^2-2g\mu ]}^{3\mathrm{/}2}}\{p(\backslash mu)=\backslash dfrac\{1\}\{2\}\; \backslash dfrac\{1-g^2\}\{\backslash left[1+g^2-2\; g\; \backslash mu\backslash right]^\{3\; /\; 2\}\}\}$$

  其中为单位距离发生次数的期望值，k 为发生次数。在此案例中，k 固定为 1，为散射系数。
  判断是否散射，通过对 P 积分得到判断是否发生散射的累计分布函数F，从0积分到自由程距离x，我们可以得到

$$F(x,\sigma \mathrm{\_}s)=\int \sigma \mathrm{\_}s{e}^{-\sigma \mathrm{\_}sx}dx\{F(x,\backslash sigma\backslash \_\{s\})=\backslash int\; \backslash sigma\backslash \_\{s\}\{e^\{-\backslash sigma\backslash \_\{s\}x\}dx\}\}$$

计算可得：

$$F(x,\sigma \mathrm{\_}s)=1-e^{-\sigma \mathrm{\_}sx}\{F(x,\backslash sigma\backslash \_\{s\})=1-\{e\}^\{-\backslash sigma\backslash \_\{s\}x\}\}$$

  同样，计算 F 对于 x 的反函数，我们可以得到自由程 x 的计算表达式

$$x=-MFP\ast \ln (1-F)\{x=-~MFP*\backslash ln(1-F)\}$$

  F 的取值范围在 [0,1]，我们可以取任意取值范围在 [0,1] 的随机数，代入 F 得到光线行进的自由程。
  通过比较光线行进的自由程，和光线距离物体表面的距离，我们可以判定光线有没有发生散射，从而选择是否需要体散射采样。
  体散射采样的方向是根据 Henyey-Greenstein 散射的相函数，Henyey-Greenstein 散射的相函数（Phase function）为：

$$P(\theta )=\frac{1-g^2}{4\pi (1+g^2-2g\cos \theta {)}^{1.5}}P(\backslash theta)=\backslash dfrac\{1-g^\{2\}\}\{4\backslash pi(1+g^\{2\}-2g\backslash cos\backslash theta)^\{1.5\}\}$$

  在 Greenstein 体散射中，散射角度取决于各向异性参数 g（Asymmetry parameter），取值范围是 [-1,1]，当 g 大于 0 表示向前散射，当 g 为 1 的时候，表示全部只会向正前散射，也就是说此时不发生散射。当 g 小于 0 时表示向后散射，当 g 为 -1 时，表示光线全部只会反向散射。当 g 为 0 时，是各向同性散射（各方向概率相同）。因此在不发生体散射的情况下，我们通常将 g 的默认值设为 1。
  由于 Henyey-Greenstein 是一个根据经验得到的散射模型，的数值通常可以通过以下公式在现实中拟合得到：

$$g\mathrm{\_}1=\int \mathrm{\_}{0}^{2\pi }\int \mathrm{\_}{0}^{\pi }P(\theta )\cos \theta \sin \theta d\theta d\varphi g\backslash \_\{1\}=\backslash int\backslash \_\{0\}^\{2\backslash pi\}\backslash int\backslash \_\{0\}^\{\backslash pi\}P(\backslash theta)\backslash cos\backslash theta\backslash sin\backslash theta\{d\}\backslash theta\{d\}\backslash phi$$

  该值代表散射角余弦值的期望值。
  粒子透射率是指在每一次散射的采样中，相对功率的损失，相对功率和粒子透射率的关系为：

$$P^{\mathrm{\prime }}=P\ast TP^\backslash prime\; =\; P\; *\; T$$

  在实际应用中，Henyey-Greenstein 散射常被用来绘制后向散射曲线，并进行相似性分析。后向散射曲线的典型应用场景，如图，图中红色点为光源，外围蓝色球体为远场探测器

  Henyey-Greenstein 后向散射曲线描述了光线散射的方向分布。其中横坐标 (x轴) 通常是散射角 θ。这个角度是入射光线和散射光线之间的夹角，范围从 0° 到 180°。其中，0° 表示完全的前向散射，而 180° 表示完全的后向散射。纵坐标 (y轴) 是相对于散射角 θ 的散射强度或散射概率，在这里由 Henyey-Greenstein 相函数 P(θ) 给出。

3 软件功能支持

  为了帮助工程师和科学家有更直观方便的仿真体验，我们提供了

• 1.基本的 Henyey-Greenstein 体散射的光线追踪，可以通过直接指定平均自由程，各向异性参数，以及粒子透射率，或者间接指定相关的参数（如散射系数，约化散射系数，缩放平均自由程等），对光线通过包含符合 Greenstein 模型的粒子的物体时，产生的现象进行仿真。
• 2.对材料指定波长的光线进行散射参数计算理论值的快速预览功能，包括查看散射曲线，对上例中其他各项参数进行插值，计算和显示的功能。
• 3.对单条光线的散射轨迹进行追踪和高亮，对光线外的物体进行透明化等配套功能。

4 仿真设置

  首先我们建立一个物体作为散射的样本，物体的位置和几何信息如下

Geometry Type	Radius	Height	Taper	(x,y,z,α,β,γ)
Cylinder	5mm	20mm	1	(0,0,0,0,0,0)

  全部表面的光学属性为 perfect_transmitter

  该圆柱体的材料为某折射率为 1，透射率为 1 的气体样本，其中掺入有以 Greenstein 为散射模型的粒子，我们将材料类型设置为各向同性,粒子体散射类型设置为 Henyey-Greenstein 之后，就可以对我们的散射特性进行编辑了。

  散射特性的各项参数设置如下：

一、平均自由程

  在对平均自由程的设定中，我们支持三种设定方法，分别是对平均自由程直接输入，对散射系数的输入，以及对约化散射系数的输入。在这里我们简单选择输入平均自由程。同时平均自由程的缩放系数被设置为默认值 1。输入的波长和平均自由程的表格如下：

Wavelength(nm)	Mean Free Path(mm)
545	0.08
555	0.12

二、各向异性参数

  输入的波长和各向异性参数的表格如下：

Wavelength(nm)	Anistropy Factor
540	0.7
560	0.6

三、粒子透射率

  输入的波长和粒子透射率的表格如下：

Wavelength(nm)	Particle Transmissivity
555	0.8

  我们使用的光源的信息如下：

Source Type	Radiant Power	(x,y,z,α,β,γ)
Point Source	1W	(0,0,-0.1,0,0,0)

  我们设定光源的发射角为 0 度，θ 和 φ 角也都为 0 度，这表示光线沿着 z 轴垂直入射该散射介质。光源所发射光线为单波长，波长为 550nm。

  我们使用平面探测器的设置信息如下：

Geometry Type	Length	Width	(x,y,z,α,β,γ)
Rectangle	10mm	10mm	(0,0,-2,0,0,0)

  另外我们使用一个远场探测器以观察散射的角度分布

5 结果分析

  如图所示是平面照度探测器的显示结果

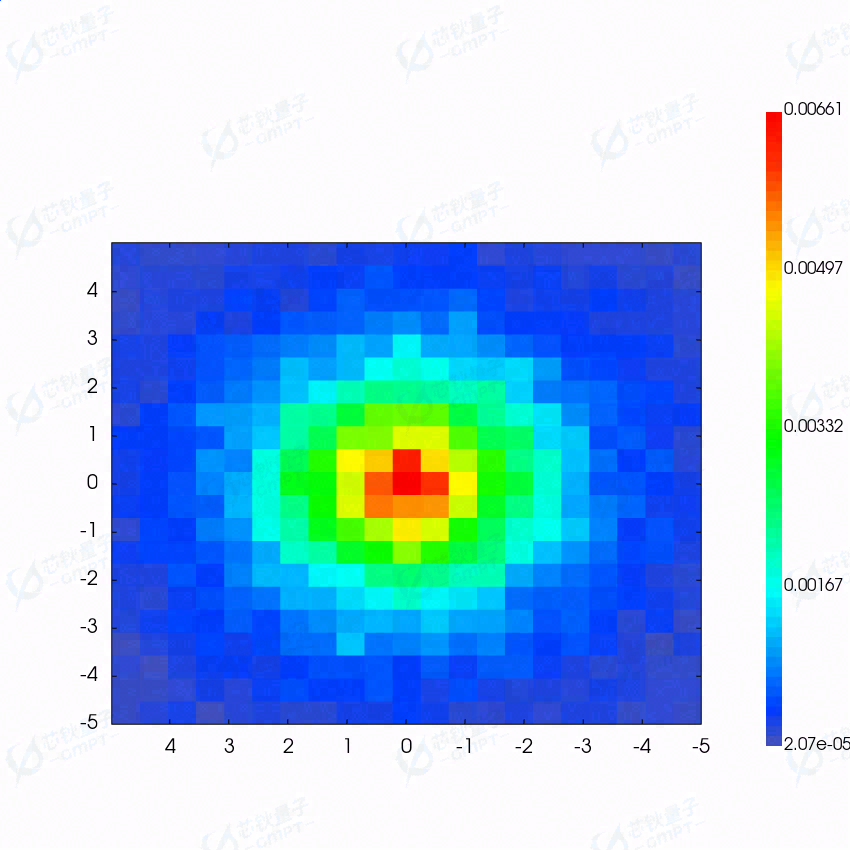
  3D 图示如下，纵坐标代表照度大小

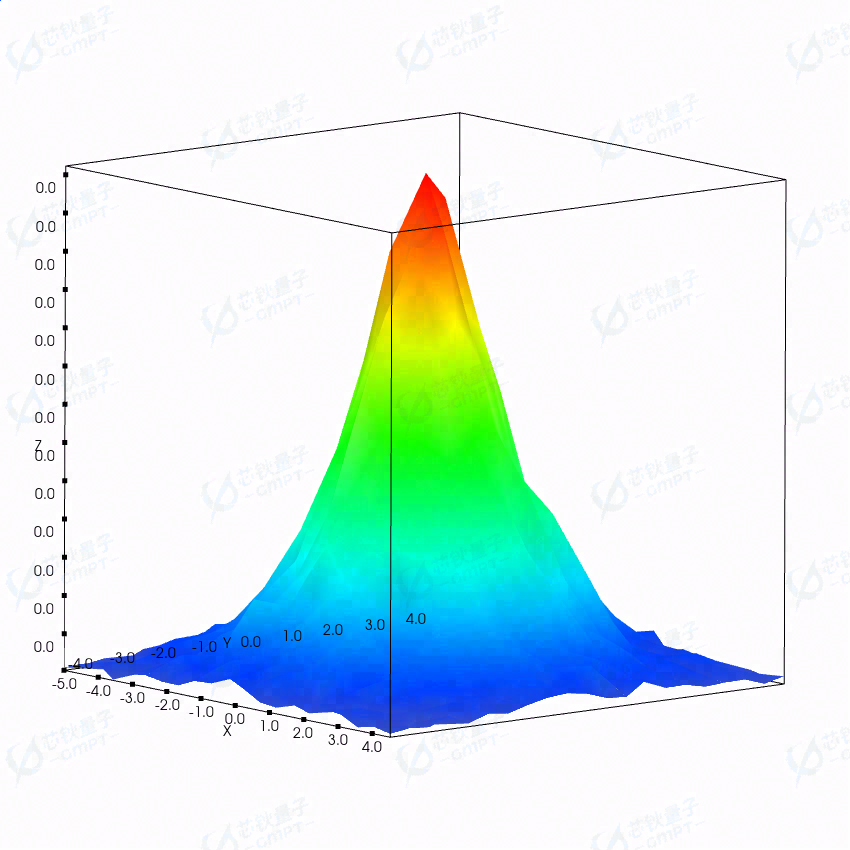
  远场接收器的结果如下：

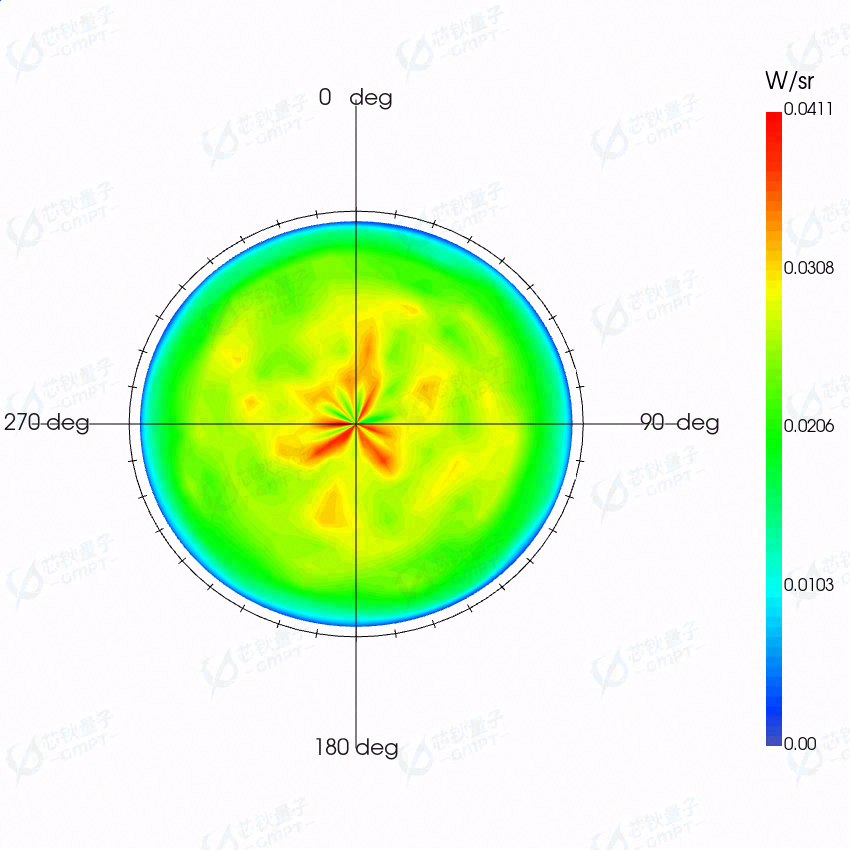
  根据 Greenstein 对于散射各向异性参数的定义，散射角为 0 度时，即中央区域往往都有着最大的散射概率。

  下表是 550nm 散射曲线的各项参数：

Property	Value
wavelength	550nm
Mean Free Path	0.1mm
Scatter Coefficient	10
Reduced Scatter Coefficient	4
Average Cosine	0.65
Gamma	1.65

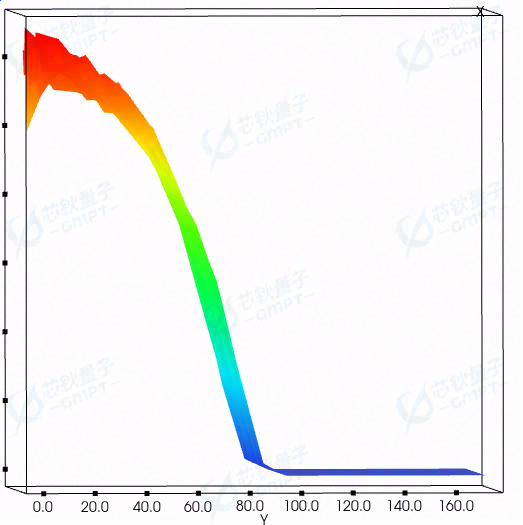
  我们界面上根据相函数得到的 550nm 散射曲线如下：

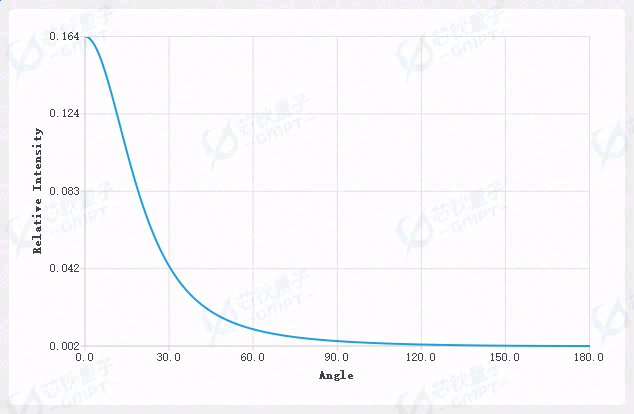
  在实际仿真十万条光线之后，我们可以根据三维卡式坐标图的侧面视角，得到实际的散射曲线。

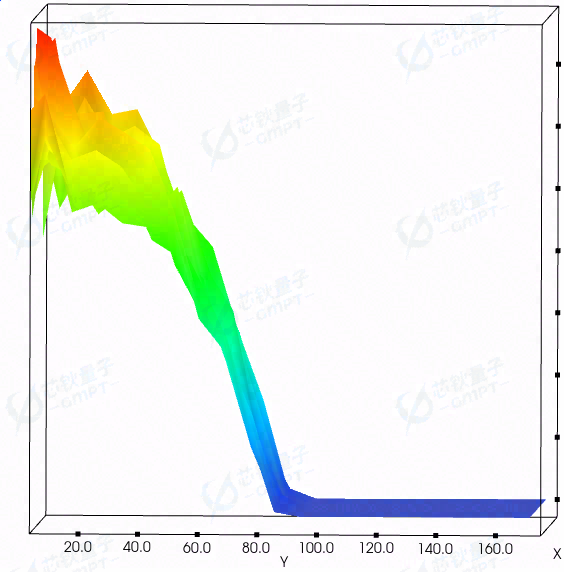
  而在将仿真光线数量提升到 100 万条之后，我们可以得到更加收敛且平滑的结果。