使用 Rayzen 软件优化分叉光导
1.背景介绍
集光系统和导光系统的设计是光学系统设计的重要组成部分。集光系统设计的主要目标是提高光能的传输效率,减少光能在传输过程中由于反射、散射、吸收等引起的损耗。导光系统设计的主要目标首先是要将光能传输到期望的位置,其次是要尽量减少光能在传输过程中由于反射、散射、吸收等引起的损耗。
分叉光导是一种常见的集光系统,它可以将光能均匀地分配到多个光导中,从而提高光能的传输效率。这种光学结构可以用于地下室或地铁站照明,由于全程通过将自然光引入室内,因此可以大大减少能耗,对实现绿色照明和碳中和目标具有积极意义。
本文使用 Rayzen 软件对分叉光导系统进行优化设计,以实现光能的高效传输和减少光能的损耗。
2. 性能指标
集光与导光系统的性能指标主要包括光能传输效率和到达传输目标位置时的均匀性,在 Rayzen 软件中,我们可以通过以下参数来评估这些性能指标:
- 光能传输效率:通过计算两个接收器处接收的功率来衡量,数值越大表示光能传输效率越高。光源的相对功率为 1W,我们希望在光线传输过程中的损耗尽可能地少,由于本案例为平面对称的结构,我们只需要计算一个接收器处的功率即可,目标值为 0.5.
- 均匀度:通过计算两个接收器处得到的光能到达传输目标位置时的光强分布来评估,数值越均匀表示光能到达均匀性越好,均匀性的评价指标可以通过计算接收器上光强分布的标准差来衡量,目标值为 0.0.
根据以上指标构建如下评价函数: 其中, 和 分别为两个指标的权重,默认为 1, 为接收器处接收的功率, 为接收器上光强分布的标准差。
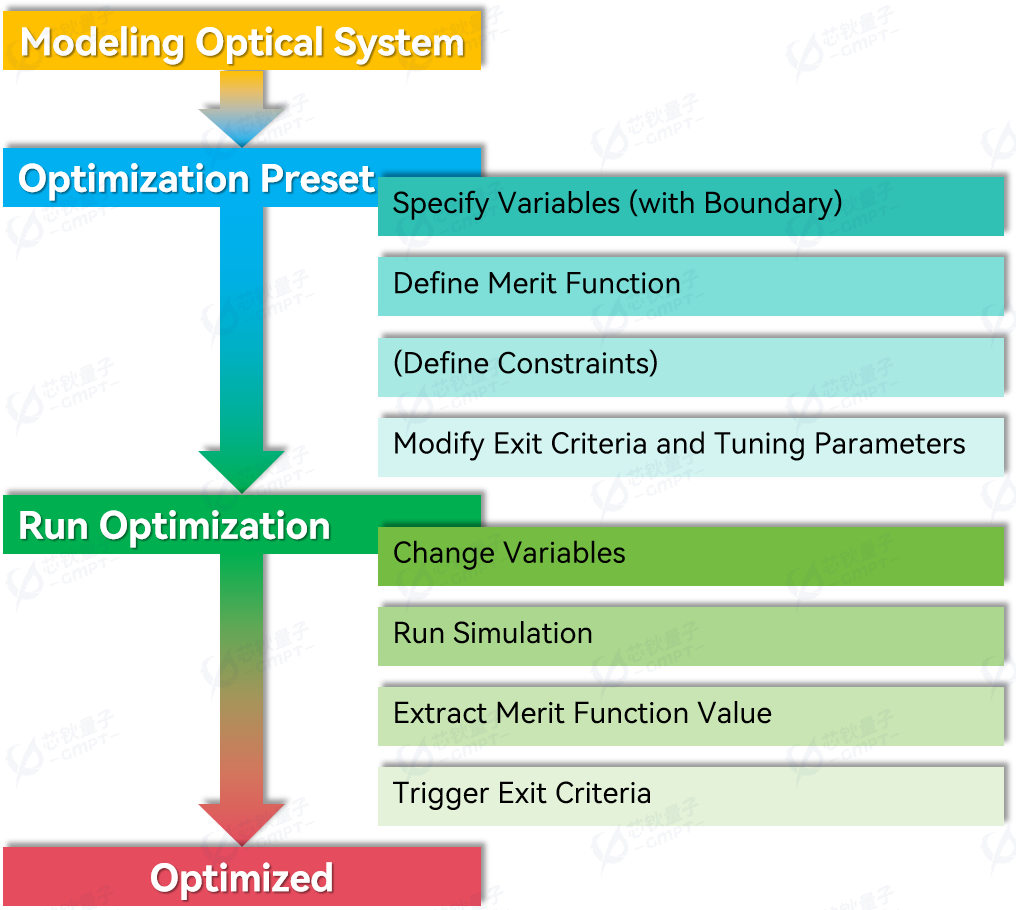
3. 优化流程
使用 Rayzen 软件对分叉光导系统进行优化设计,以实现光能的高效传输和出光位置的均匀分布。优化流程如下:
4. 模型构建
如图 [2] 为分叉光导系统示意图,其中,光源为点光源,发散角度为 30°,接收器为两个平面,分别位于光导的两侧,光导的材质为 PMMA。光线在光导内部以全反射的方式传播,最终在接收器处收集光能。
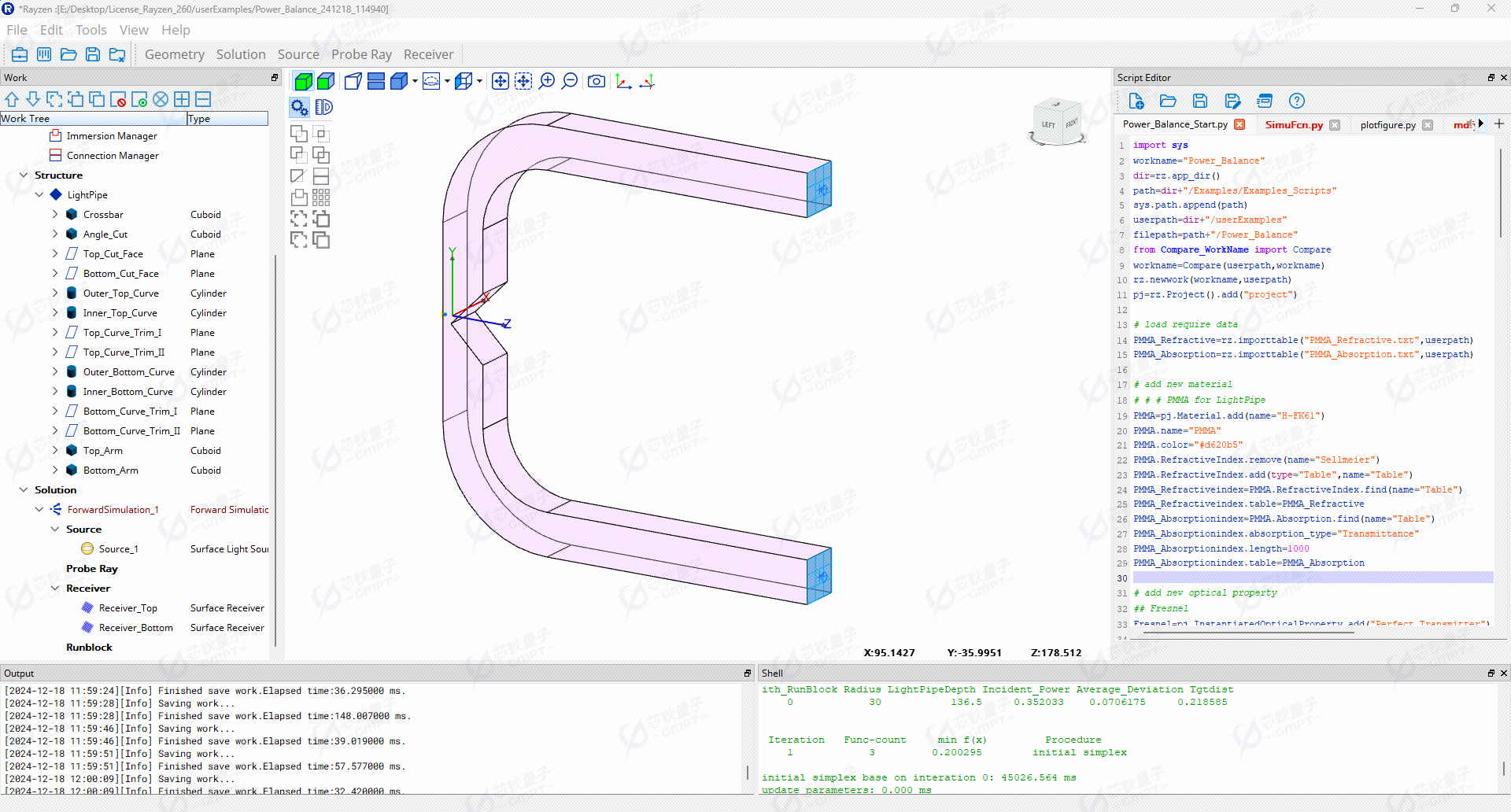
5. 优化模型与参数设置
本案例使用单纯形方法对光导的弯曲半径和臂长进行优化。Nelder-Mead 单纯形算法是一种用于在多维空间中寻找函数最小值的数值优化方法。该算法不依赖于目标函数的梯度信息,因此非常适合用于那些难以计算或定义梯度的优化问题。
这种方法根据给定的初始猜测,构造一个初始单纯形。通过轻微改变初始猜测中的每个维度来创建额外的顶点,从而形成一个 n 维空间中的 n+1 个顶点构成的单纯形。算法通过计算单纯形中每个顶点的目标函数值,选择出目标函数值最小的顶点作为当前最优解,并调整单纯形的位置以逼近最优解。在每次迭代中,算法通过反射、扩展、收缩和缩小等操作来调整单纯形的位置,直到达到收敛条件为止。每种操作都有其特定的条件和目的:
1. 反射(Reflection)
改进依据:当反射点 xr 的目标函数值优于最差点但不如最佳点时,说明单纯形可以通过这个新的点来改善。反射操作旨在通过“镜像”最差点关于剩余点的质心,寻找更好的位置。
公式: 其中, 是除了最差点以外所有点的平均位置, 是反射系数,默认值为 1.
2. 扩展(Expansion)
改进依据:如果反射点 xr 的目标函数值非常好,甚至比当前的最佳点还要好,那么可以进一步尝试沿反射方向扩大步长,以期找到更优的点。这是为了加速收敛到最优解的过程。
公式: 这里, 是扩展系数,默认值为 2。
3. 收缩(Contraction)
改进依据:如果反射点 xr 的表现不佳,即它的目标函数值并不比最差点好,那么需要采取更加保守的方法。收缩操作分为两种类型:
- 外部收缩:当反射点介于最差点和次差点之间时使用。
- 内部收缩:当反射点比最差点还差时使用。这种情况下,收缩点靠近质心,目的是避免过度偏离可能的最优区域。
公式:
- 外部收缩:
- 内部收缩: 这里,,默认值通常为 0.5。
4. 缩小(Shrink)
改进依据:当上述三种操作都不能有效改善单纯形时,意味着单纯形可能已经包围了局部极小值或遇到了困难。此时,缩小操作会将所有顶点向最佳点靠拢,这有助于重新调整单纯形的形状,以便更好地适应新的搜索空间。
公式: 这里,,默认值通常为 0.5。
6. 优化结果与分析
6.1 机理分析
我们首先从理论出发,分析变量与评价指标的关系,为优化方向提供理论依据。
- 接收器接收功率应随随半径的增大而增长,这是由于过小的半径会导致光导的弯曲过大,全反射条件不满足的区域较大,导致过多的光线泄漏。
- 接收器上光强分布的标准差应随臂长的增大而减小,并逐渐趋于稳定,根据匀光棒的原理,不同入射角的光线经过多次全反射,每次反射都会形成一个新的虚拟光源像,并且这些虚拟光源像是叠加的。当通光管长度增加时,光线有机会进行更多的反射,这增加了不同方向上光线混合的机会,从而提高了光的均匀度。有时光路可能形成特定的周期性条件,随着长度的增加,均匀性呈现震荡上升。
- 接收器接收功率应随臂长的增大而减小,这是由于材料内部的吸收和散射效应,随着臂长的增加,光在材料内部的传播距离增加,导致更多的光被吸收和散射,从而降低了接收功率。对于高透过率材料,这一效应不会是主因,因此不在主要的优化方向参考中。
- 接收器上光强分布的标准差与半径间缺乏显著的直接关联,难以从物理意义上直观地解析它们之间的内在联系。进行优化设计时,我们更倾向于关注那些具有明确因果关系及可预测影响的因素,以确保优化过程的有效性和可靠性。鉴于此,在主要优化方向的考量中,该关系并未作为重点参考因素。
6.2 参数扫描
如果模型的初始值给得足够好,那么优化方法可以快速收敛到最优解。然而,如果初始值不佳,可能会陷入局部最优解,而不是全局最优解。因此,条件允许的情况下,我们通过参数扫描方法,寻找足够好的初始值,从而使得单纯形方法能够更快地找到全局最优解。
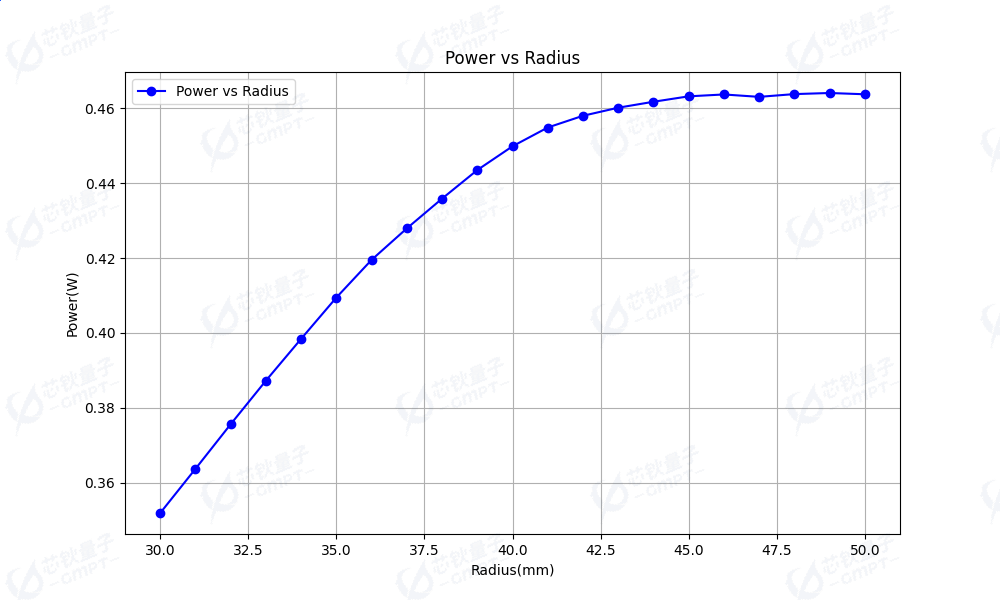
如图 [3] 所示为接收器接收功率与半径的关系随迭代次数的变化趋势,可以看到接收功率随半径的增大而增长,从半径大于 40mm 开始,接收功率的增长开始变缓。这符合理论分析 1. 在梯度下降优化方法中,我们可以选择半径为 40mm 作为初始值,从而使得优化方法能够更快地找到全局最优解。
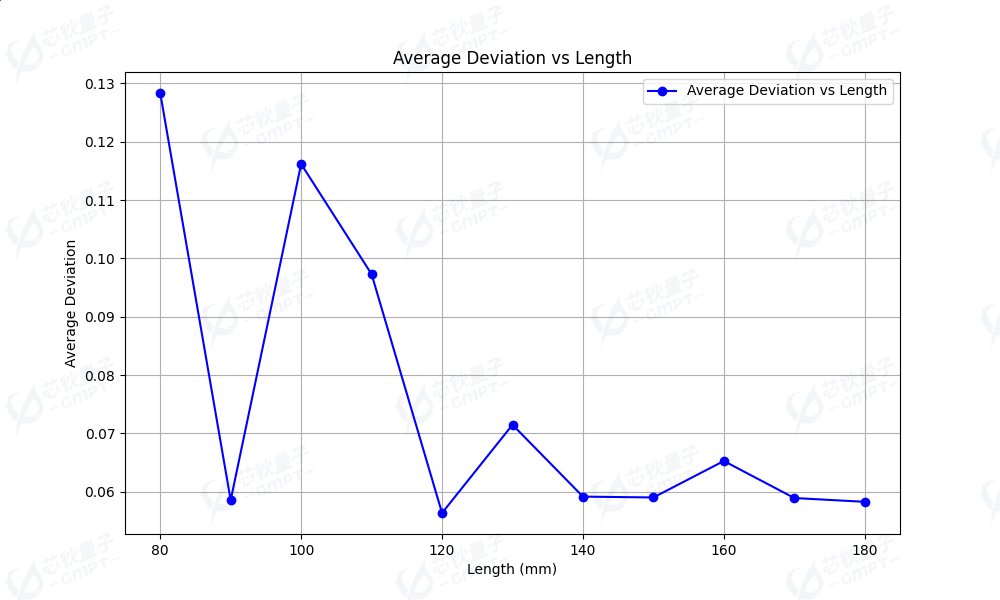
如图 [4] 所示,接收器上光强分布的标准差与臂长的关系随迭代次数的变化趋势,可以看到标准差随臂长的增大而震荡降低,从臂长大于 140mm 开始,标准差波动开始变缓。这符合理论分析 2. 在梯度下降优化方法中,我们可以选择臂长为 140mm 作为初始值,从而使得优化方法能够更快地找到全局最优解。
6.3 单纯形优化
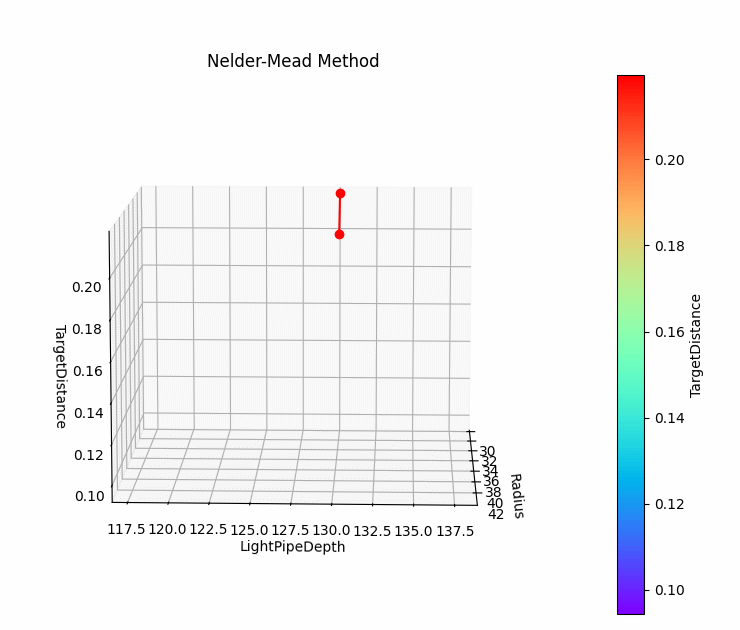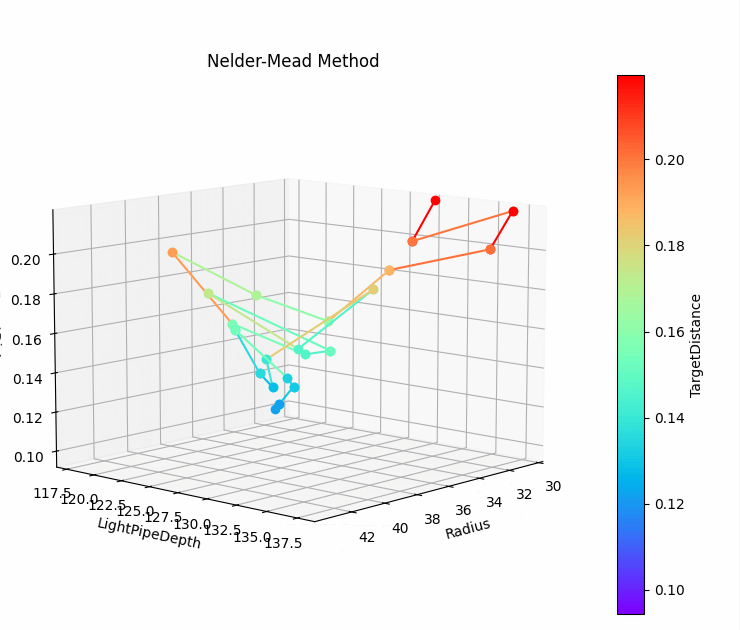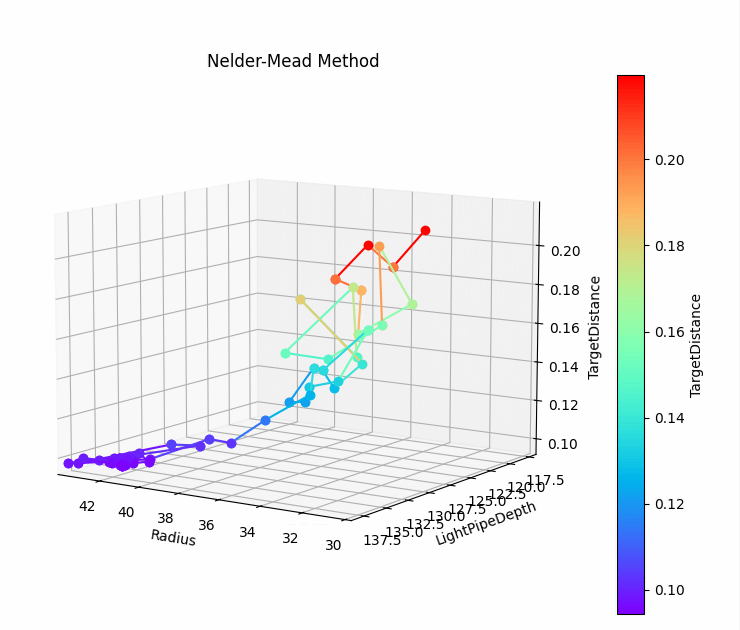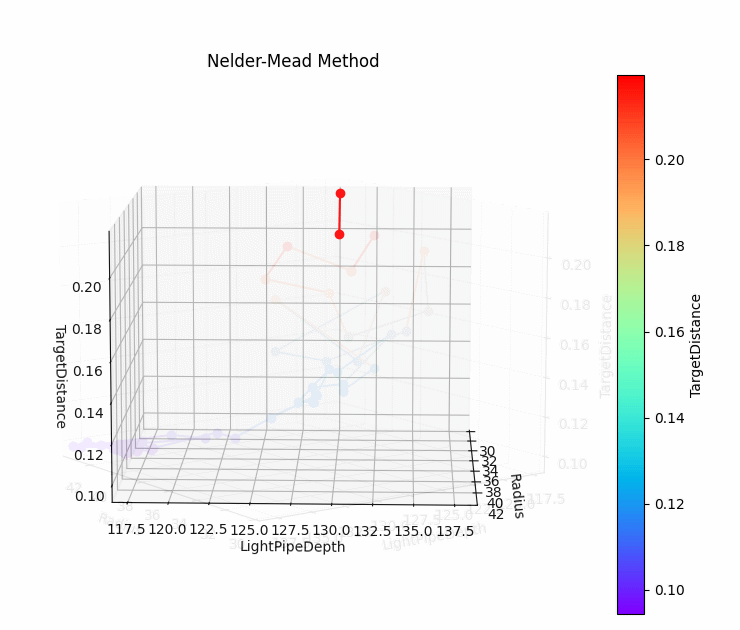
如图 [5] 所示为未选择初始值,通过单纯形法优化得到最优解的过程,从半径为30mm,臂长为130mm出发,经过15次迭代,评价函数趋于收敛,并在第32次迭代,通过收敛判据结束迭代。
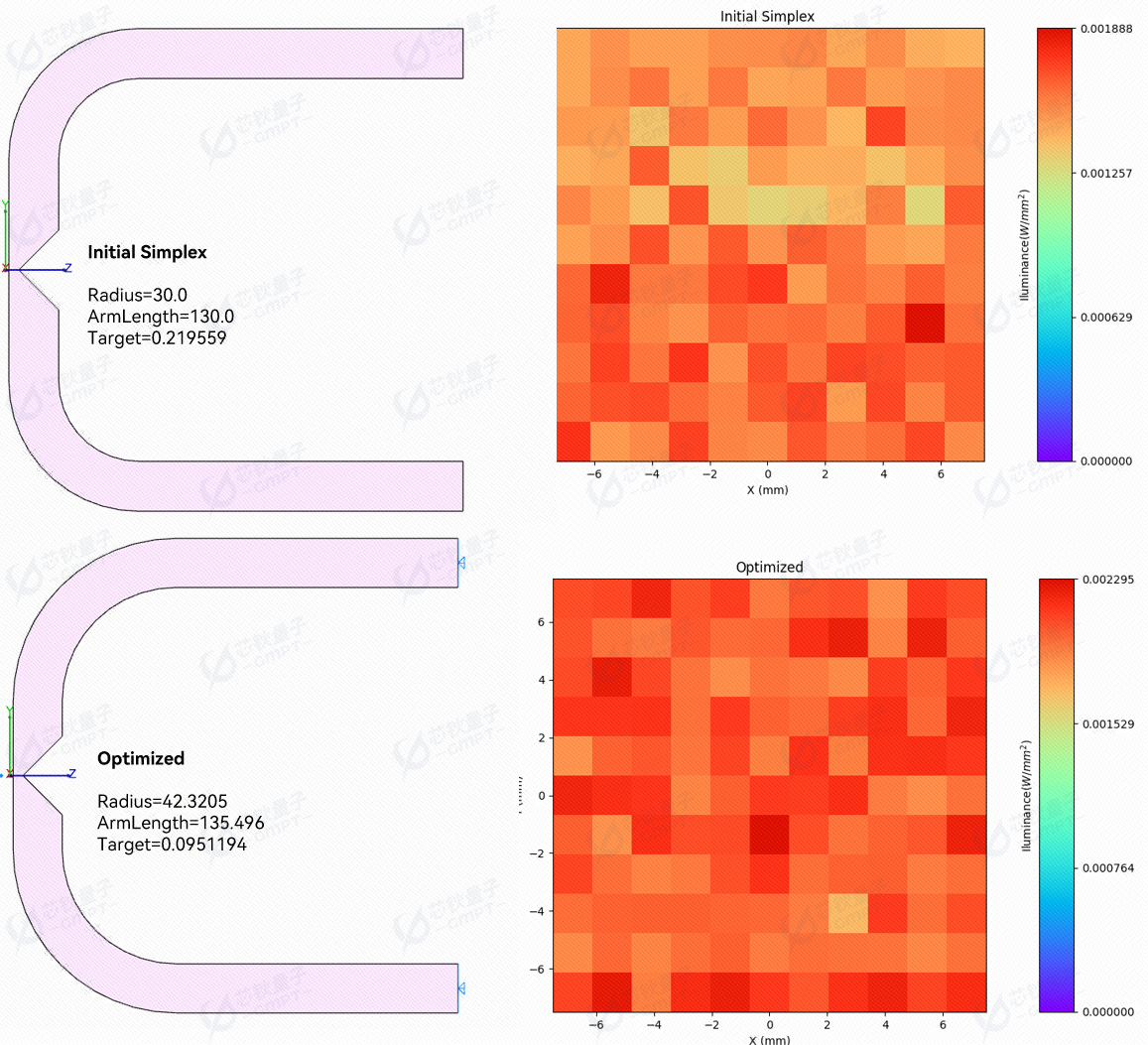
如图 [6] 所示为分叉光导优化前后结构与接收器照度分布对比,可以看到优化后,接收器上接收光能更多,光强分布更均匀,从而提高了分叉光导系统的性能。
7. 结论与展望
本文使用 Rayzen 软件通过单纯形方法对光导的弯曲半径和臂长进行优化,从而得到最优的设计方案。通过理论分析,确定扫描的参数对象,并选择合适的初始值,为优化方向提供理论依据。优化结果与理论分析一致,优化结果显示,通过单纯形方法优化得到的分叉光导系统具有更高的接收功率和更均匀的光强分布,从而提高了分叉光导系统的性能。仅对于本案例而言,由于参数空间定义清晰,使用梯度下降法可以更快地找到全局最优解,但单纯形方法对于参数空间定义不清晰的案例,可以提供一种更稳健的优化方法。接下来,我们将继续探索其他优化算法,如遗传算法、粒子群优化算法等,与各类其他光学系统交叉结合仿真并进行设计,为行业提供更丰富的设计思路。