逆向设计Y-branch光波导器件

GMPT, 2024/08/29

   传统光子学器件的设计基于器件的物理原理，并通过数值模拟来进行优化。这种方法受限于预先设定的模型，设计的自由度有限。为了满足对高性能器件的需求，具有更高设计自由度的逆向设计方法得到了快速的发展。逆向设计方法能在整个参数空间中寻找最优解，从而更可能设计出性能更优异的器件。
   本文使用Macondo 软件建立Y-branch 光波导器件逆向设计模型，分别利用Nelder-Mead 和遗传算法优化Y-branch 光波导器件的轮廓并给出最佳的透射率。下图是本文Y-branch 利用优化算法逆向设计流程图。

图1. Y-branch 逆向设计流程图

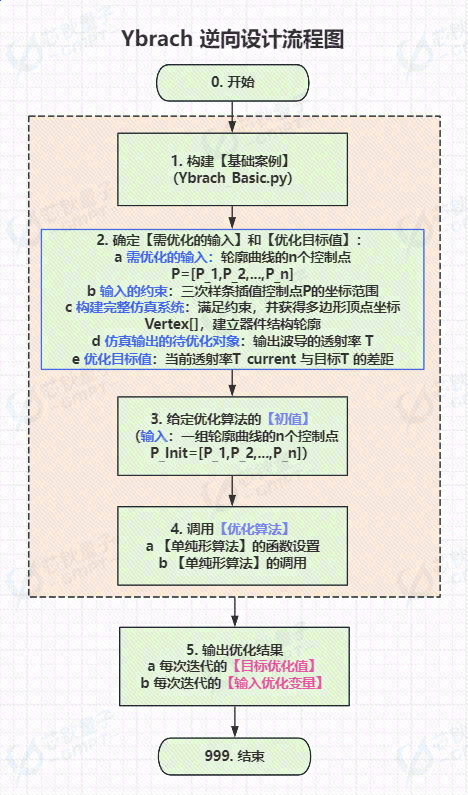
一、逆向设计器件结构介绍

   Y 分支波导（Y-branch waveguide）器件主要用于集成光路中分开（splitter 模式）或结合（combiner 模式）光路信号，或者同时兼具两者功能（bidirectional 模式）的场景 。Y-branch器件在光功分器（power splitters）、光开关（optical switches）、马赫-曾德尔调制器（Mach-Zehnder modulator）等光学器件上有广泛的应用 。
   本文的逆向设计仿真案例中，Y-branch 器件使用splitter 模式，即从单端口输入，双端口输出。通过对连接输入输出端口之间的波导结构形状进行优化，从而尽可能地使两个输出波导的功率总和接近输入功率。

1.1 器件结构的初始条件

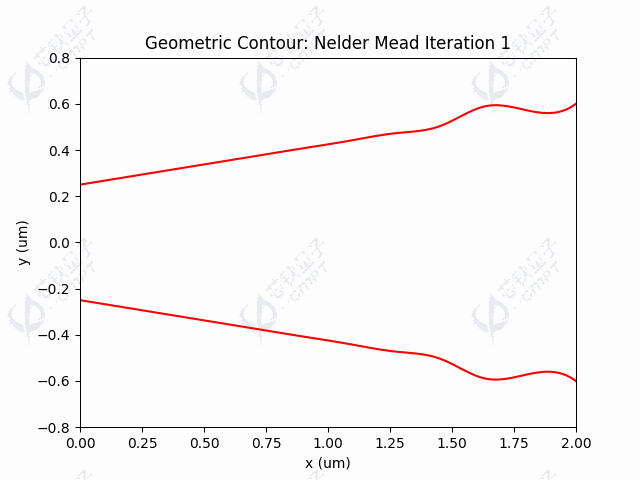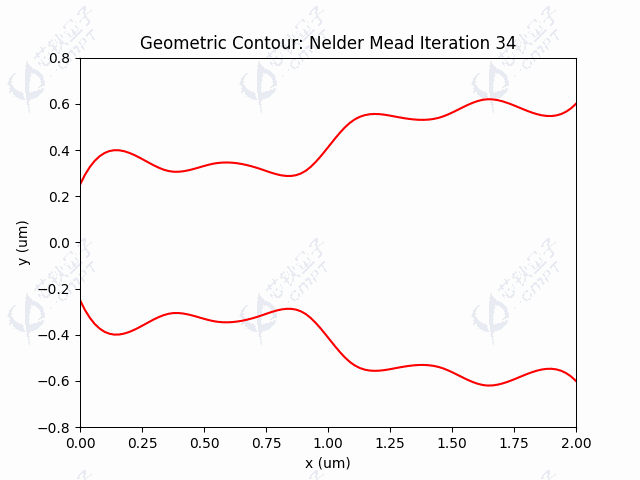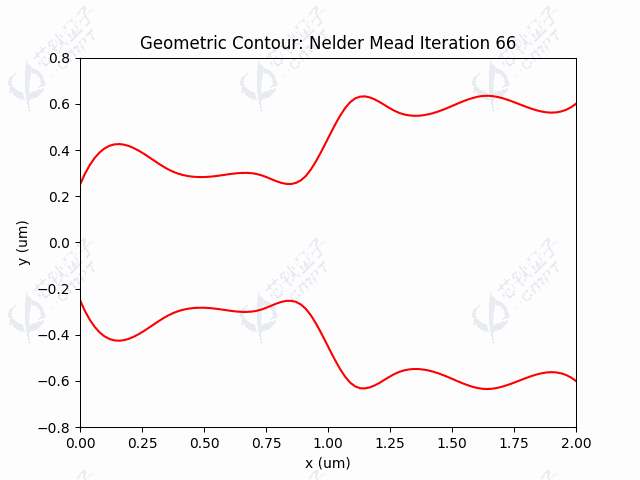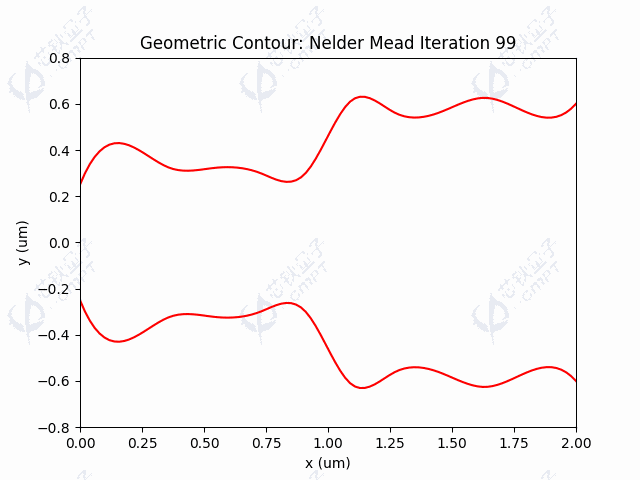
   本仿真案例中的 Y-branch 器件结构使用Si材料，包裹在SiO2材料区域中。案例中输入和输出矩形波导的长 $3\mu m3\; \backslash mu\; m$ ，宽$0.5\mu m0.5\; \backslash mu\; m$，波导厚度为$0.22\mu m0.22\; \backslash mu\; m$。两个输出端波导的间隔为$0.7\mu m0.7\; \backslash mu\; m$。对于连接输入输出端口之间的波导结构，使用多边形几何，将波导顶点相连形成边缘轮廓为直线的锥形结构，以此作为设计Y-branch 的轮廓线的初始输入。下图是Y-branch 器件设计前的初始结构。

图2. Y-branch 器件设计前的初始结构

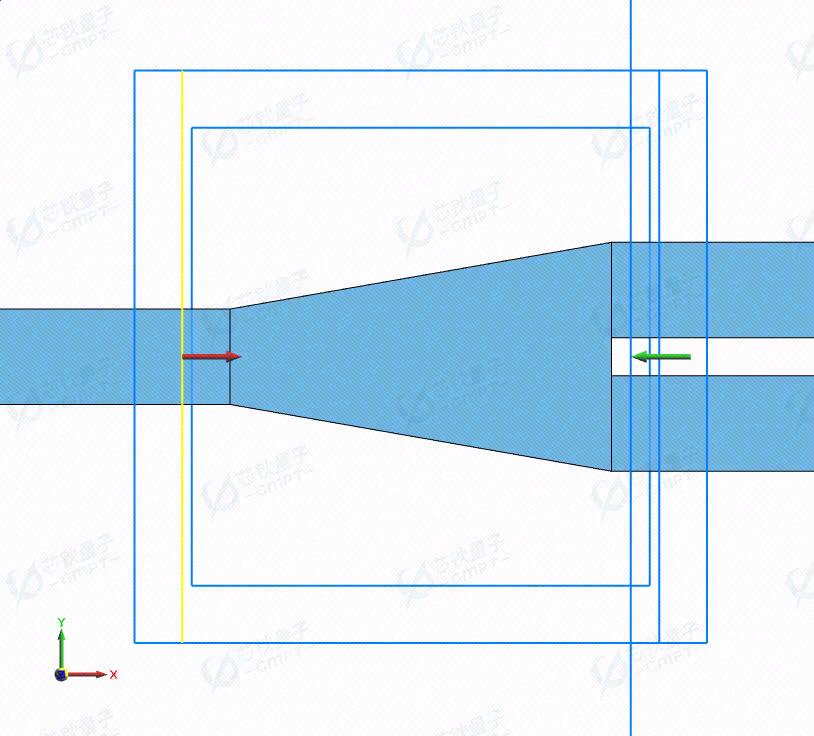
1.2 轮廓线函数的定义

   本案例中Y-branch 的轮廓线采用三次样条插值方法，是基于一组给定x 位置，生成 n 个控制点来构造一条平滑的曲线，如图 3 所示，该图展示了利用三次样条插值函数构建的曲线作为 Y-branch 器件结构的轮廓，并标出了曲线上的控制点。更多的控制点意味着更小的曲率半径对整体轮廓形状进行更细致的控制，实际中，制造工艺会限制最小的特征尺寸。大量的控制点参数会需要更长的时间来完成优化仿真。

图3. 三次样条插值函数曲线作为Y-branch 器件结构轮廓的示意图

   三次样条插值通过构建一系列三次多项式段来近似数据点，确保这些多项式在一阶和二阶导数上连续，从而得到平滑的插值函数。通过解线性方程组来确定这些多项式的系数，实现数据点之间的平滑过渡。
   使用scipy.interpolate 的splrep 实现三次样条插值处理过程，代码如下：

def get_pts(ys):
    global x_min
    global x_max
    global y_min
    global y_max
    xs = [x_min]
    for i in range(1, intervals):
        xs.append(x_min + i/intervals * (x_max - x_min))
    xs.append(x_max)
    ys.insert(0, y_min)
    ys.append(y_max)
    tck = interpolate.splrep(xs, ys)
    x_points = []
    y_points = []

   使用已经生成的插值曲线函数，取出采样点，作为轮廓多边形的顶点坐标，构建仿真所需的多边形结构，代码如下：

for i in range(101):
    x = x_min + i/100 * (x_max - x_min)
    y = interpolate.splev(x, tck)
    x_points.append(x)
    y_points.append(y)

   在本案例中选择$xx$ 坐标间段等分的10个控制点作为优化变量，更好的得到平滑过渡的轮廓线。并将控制的$yy$ 坐标限制在$0.2\mu m0.2\; \backslash mu\; m$到$0.8\mu m0.8\; \backslash mu\; m$之间，以保证设计范围的合理性。

1.3 优化目标的设置

   优化仿真采用1.55μm的模式光源注入，在输出波导处利用模式展开算法求解两个光波导基模的透射功率比，将该透射率与目标透射率的差值作为优化目标。两端口的基模电场分布如下图，理想的输出端口功率比输入端口的功率最大值为1，即为目标透射率。

图4. Y-branch 器件两端口的模式分布

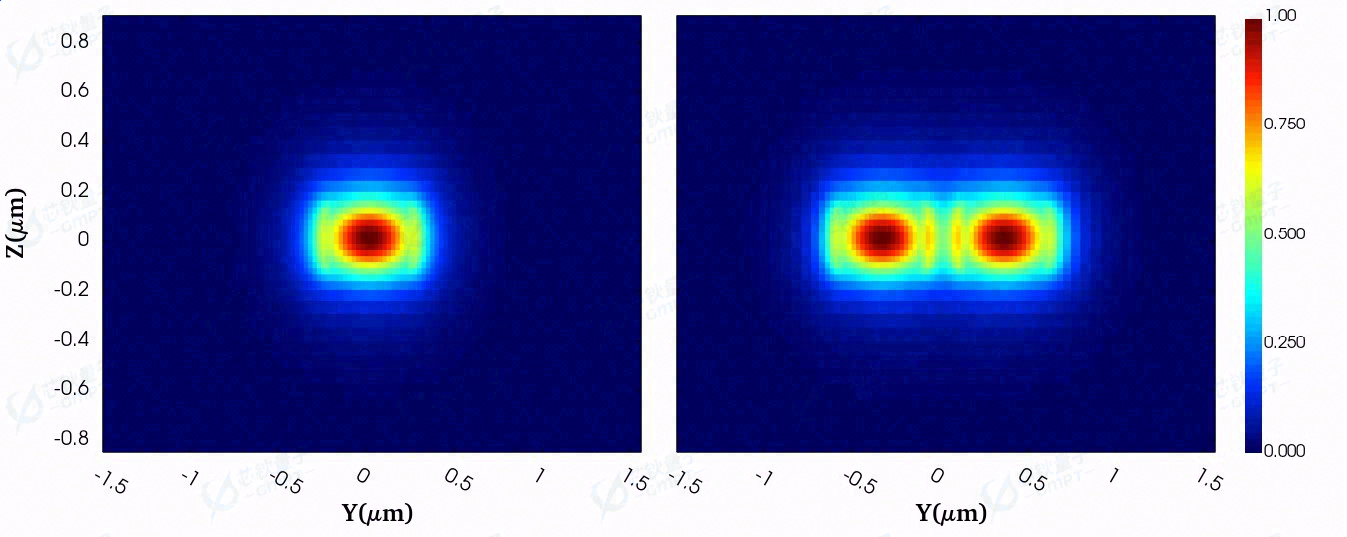
   接下来，利用优化算法对目标函数进行迭代优化，得到迭代次数内的最优解和最优目标函数值。

二、利用Nelder-Mead 算法优化器件结构

   Nelder-Mead 算法是一种无梯度的优化方法，通过迭代更新顶点形成的单纯形的多面体，并运用反射、扩张、收缩等操作来逼近多维空间中的最小值点。

图5. Nelder-Mead方法逆向设计结果 a)优化透射率关键指标的迭代过程 b)轮廓线控制点的变化过程 c)优化后的器件轮廓线 d)优化后的功率分布

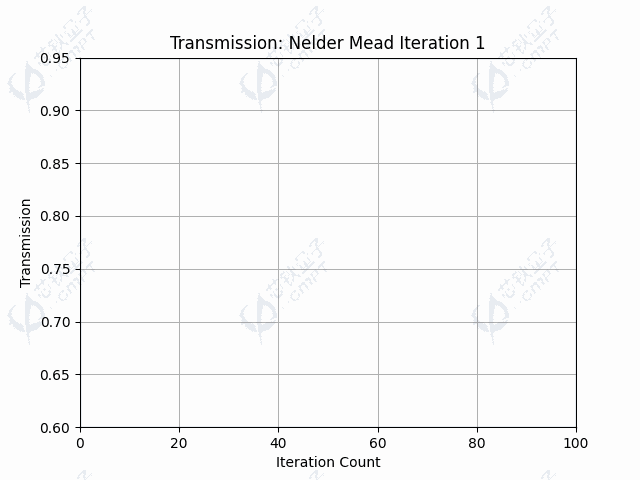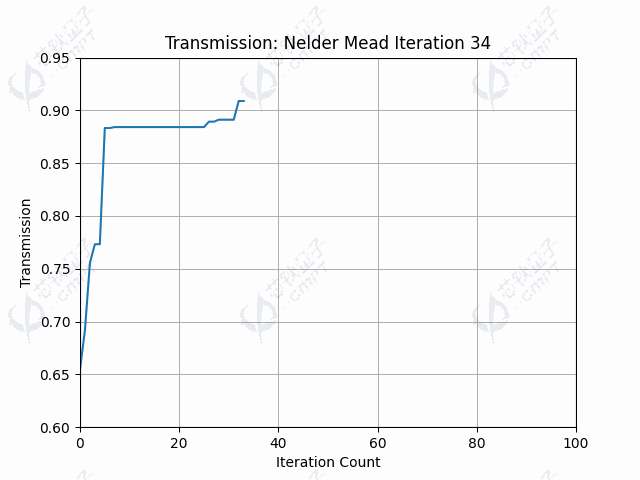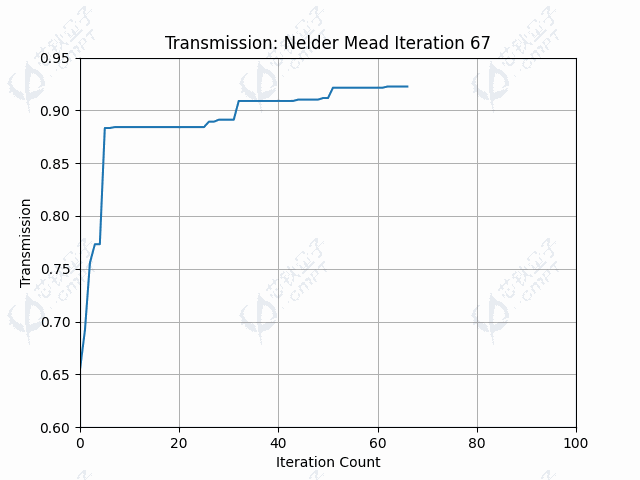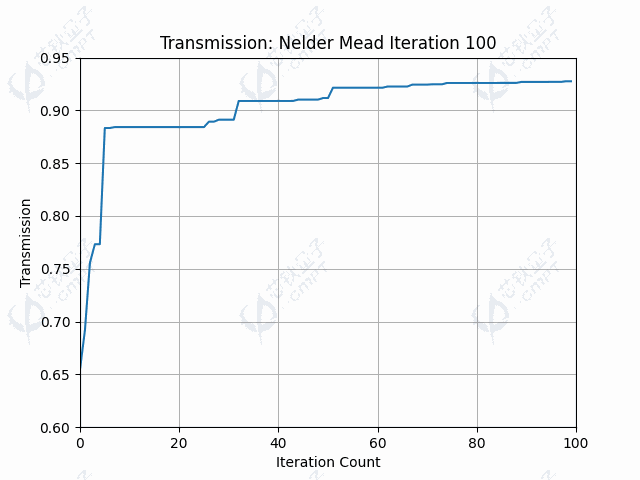
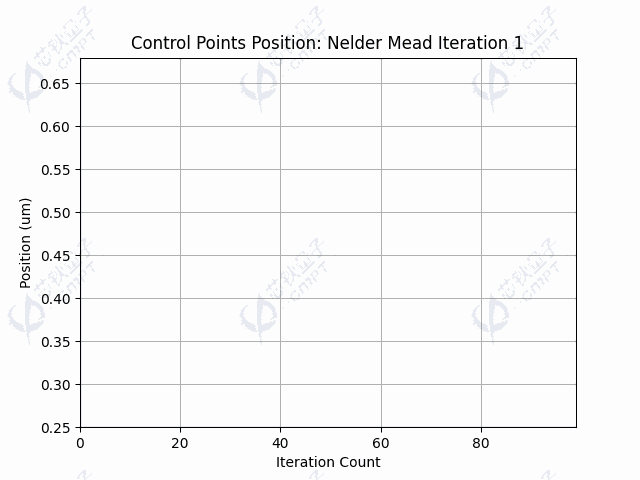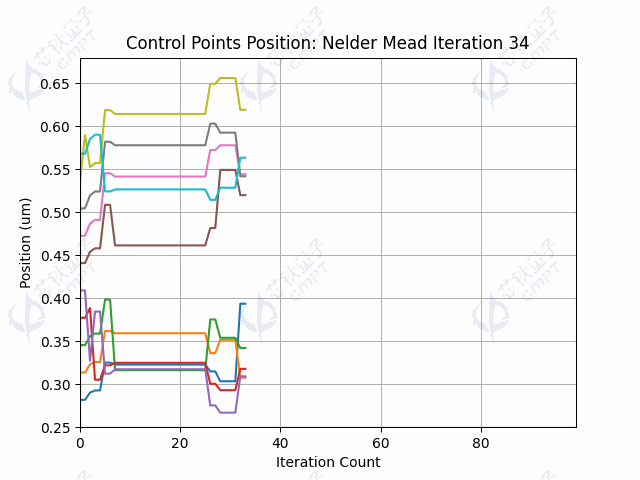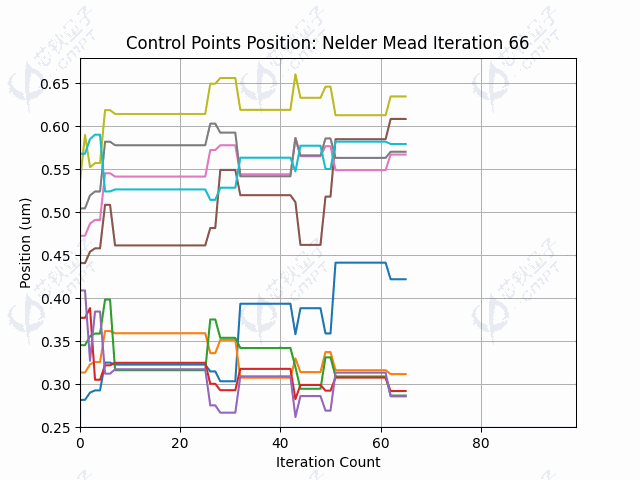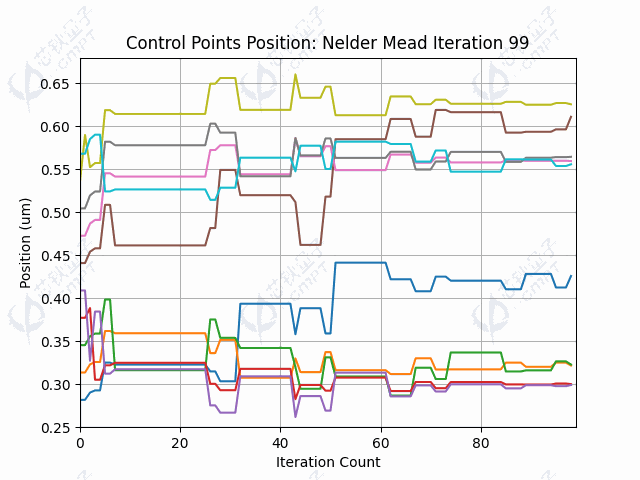
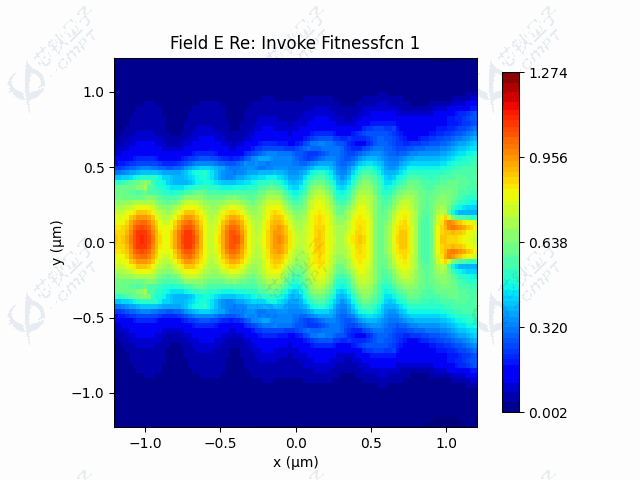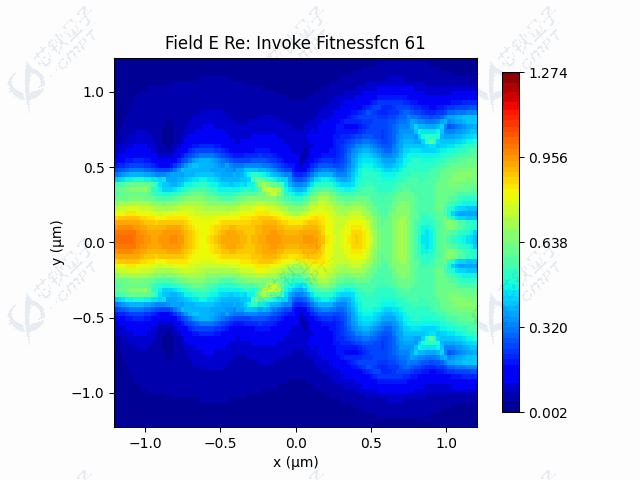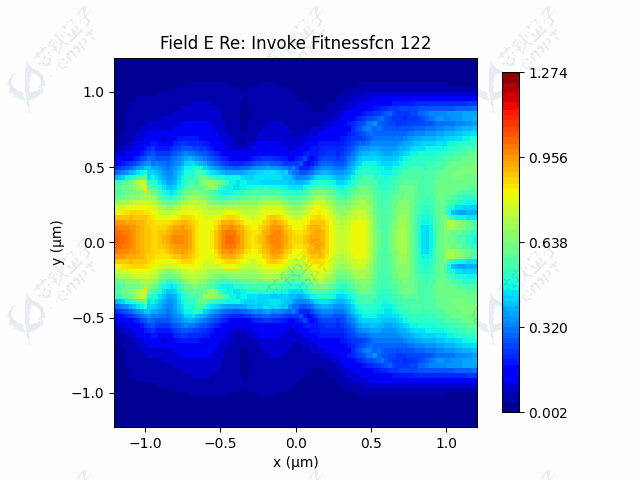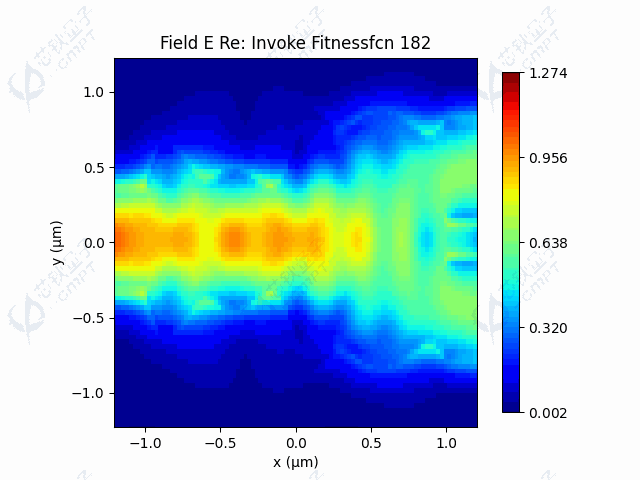
   本案例中，由于目标函数涉及调用仿真过程，调用目标函数是非常耗时的。由于Nelder-Mead方法一次迭代调用函数次数较少，因此运行时间较快。图5a展示了100次迭代的器件透射率结果，透射率最终维持在$92\mathrm{\%}92\backslash \%$左右。图5b展示了随迭代进行，轮廓线控制点的变化过程。图5c-5d展示了利用Nelder-Mead算法得到的轮廓线和场分布。

三、利用遗传算法（Genetic Algorithm）优化器件结构

   遗传算法是一种启发式搜索算法，模拟了自然选择和遗传机制来寻找优化问题的解决方案。它通过编码潜在解为染色体，并运用选择、交叉和变异等遗传操作来探索解空间。每一代中表现较好的个体更有可能被选中产生下一代，逐渐逼近最优解。

图6. 遗传算法逆向设计结果 a)优化透射率关键指标的迭代过程 b)轮廓线控制点的变化过程 c)优化后的器件轮廓线 d)优化后的功率分布

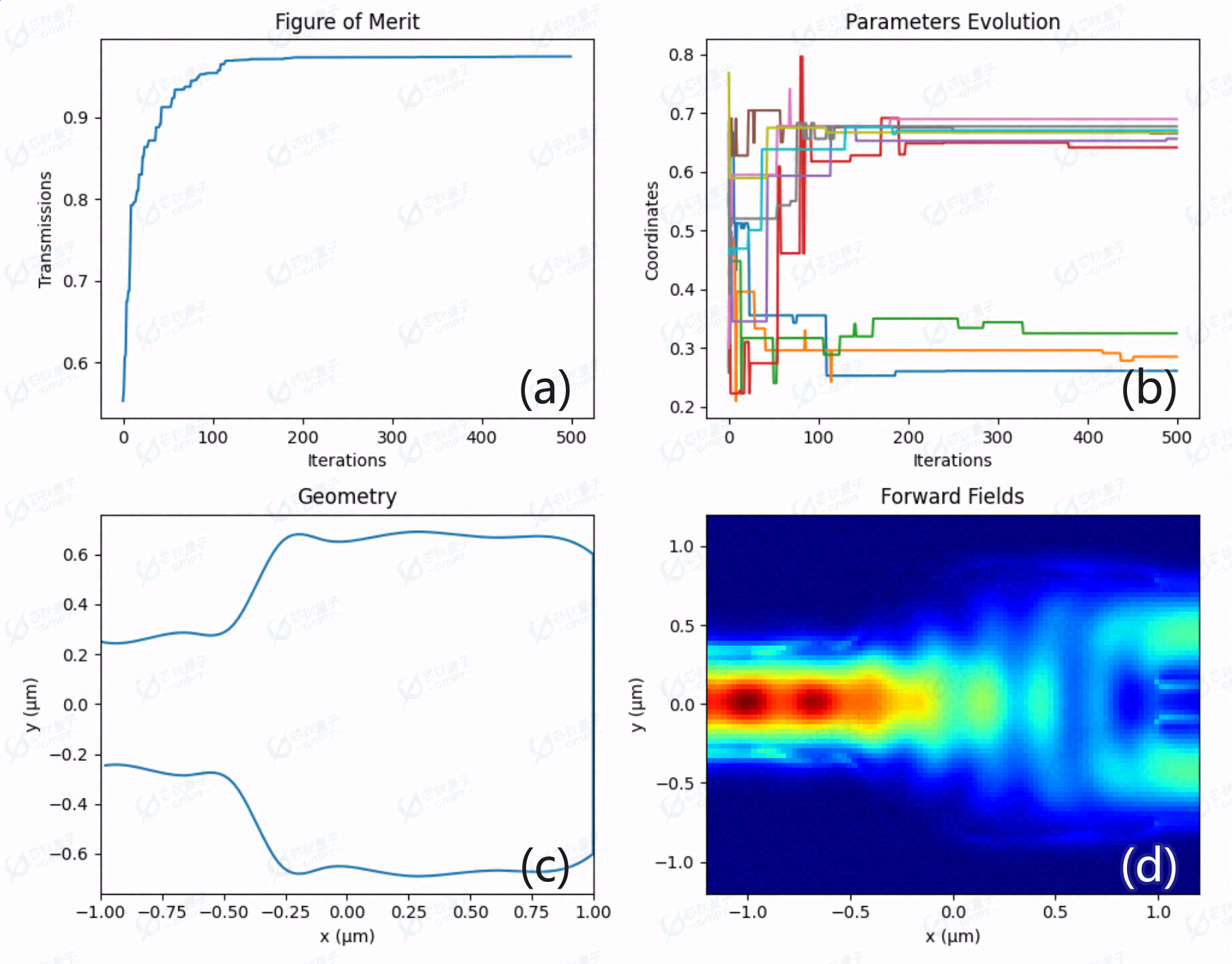
   但是每次迭代中遗传算法要调用10（优化变量的个数）次仿真，而Nelder-Mead只需要调用1次，因此，遗传算法的运行时间较Nelder-Mead 算法会更长。图6a展示了500次迭代的器件透射率结果，在迭代100次时，透射率在$96\mathrm{\%}96\backslash \%$左右，迭代200次后，透射率达到$97.5\mathrm{\%}97.5\backslash \%$。图6b展示了随迭代进行，轮廓线控制点的变化过程。图6c-6d展示了利用遗传算法得到的轮廓线和场分布。
最后，在Macondo 软件中展示逆向设计得到完整的器件结构，如下图。

图7. 逆向设计Y-branch器件结构 a)Nelder-Mead b)遗传算法

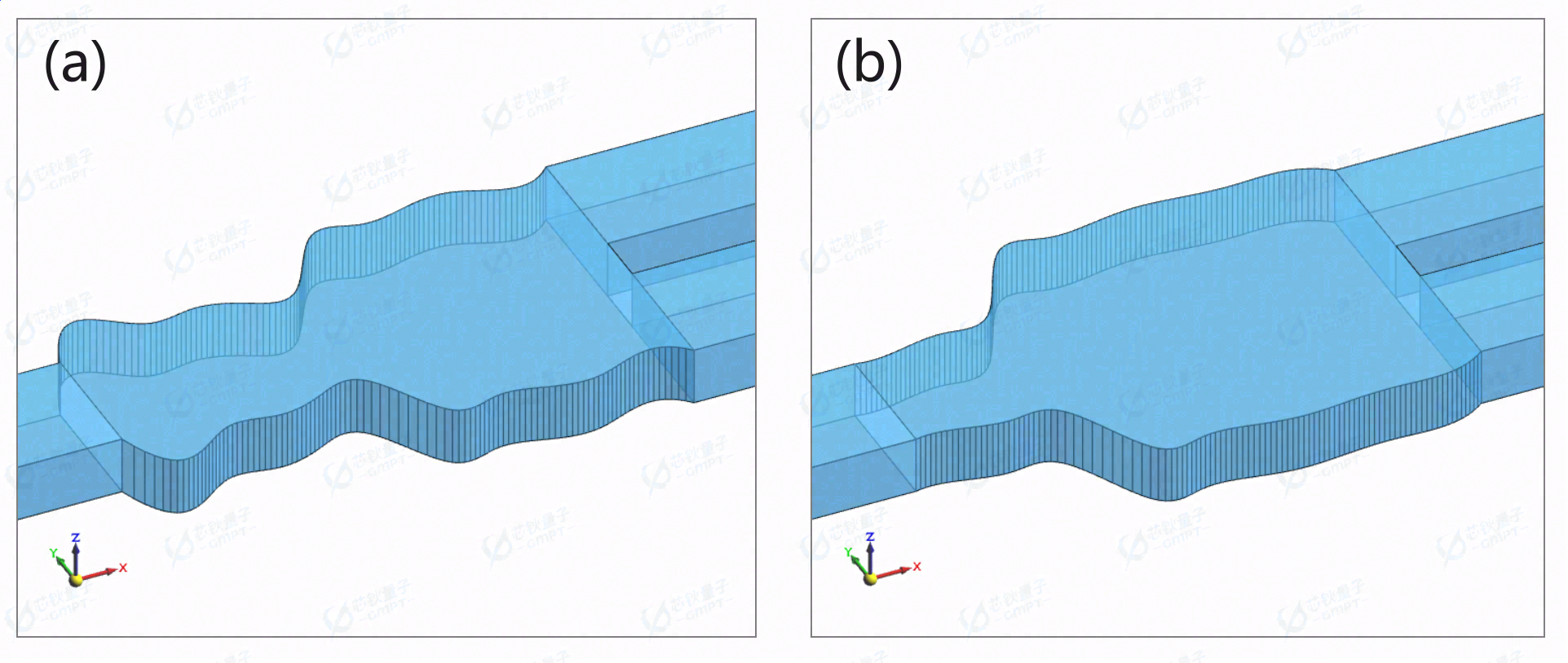
四、总结

   本文介绍了Y-branch 器件利用优化算法逆向设计的流程，通过三次样条插值函数构建Y-branch 器件结构的轮廓曲线，分别利用Nelder-Mead 算法和遗传算法优化器件结构，设计得到高透射率的器件结构。后续将对基于神经网络（neural networks）逆向设计方法和利用伴随方法（adjoint method）提高Y-branch 器件逆向设计效率的仿真进行介绍。

参考文献

[1] Hsu C W, Chen H L, Wang W S. Compact Y-branch power splitter based on simplified coherent coupling[J]. IEEE Photonics Technology Letters, 2003, 15(8): 1103-1105.
[2] Inverse design of y-branch – Ansys Optics
[3] Optimization (scipy.optimize) — SciPy v1.14.1 Manual