使用Nuwa TCAD软件仿真InGaAs HEMT器件

GMPT, 2025/3/3

注：本文和相关案例为上海芯钬量子科技有限公司与甬江实验室精准光子集成研究中心施跃春教授团队联合开发。

一、器件结构

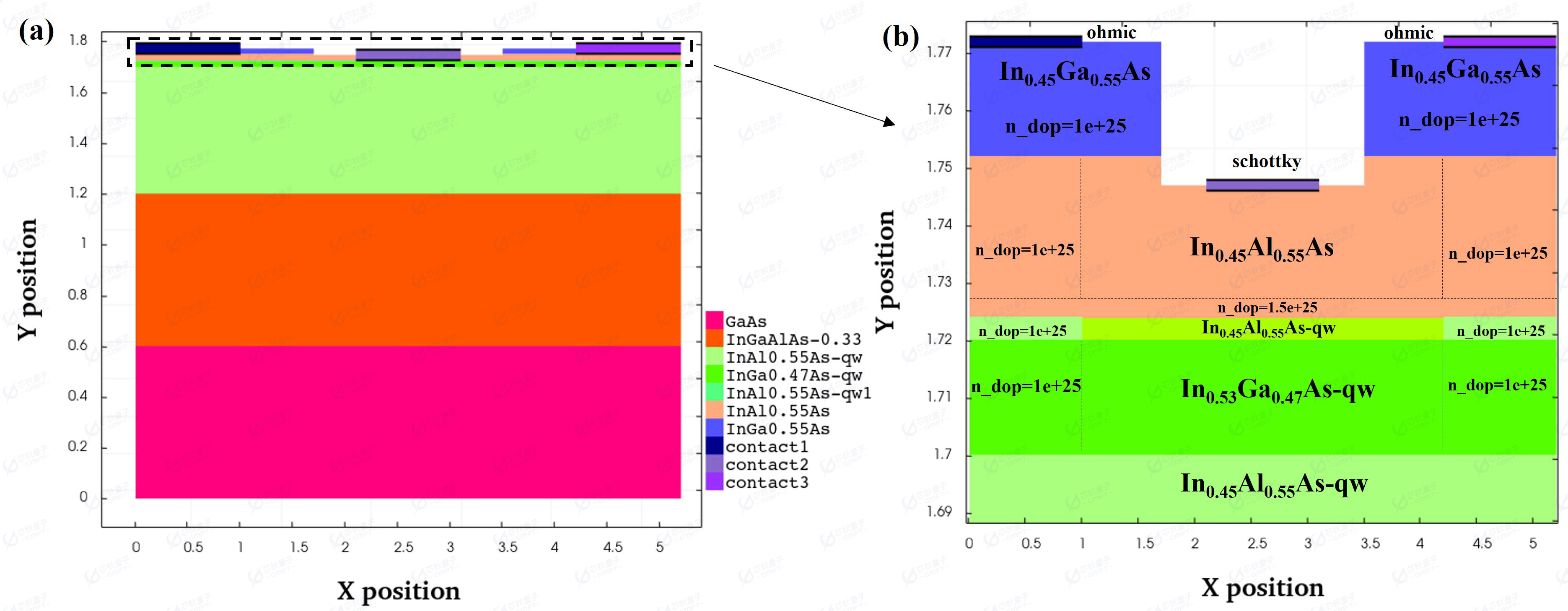
图1（a）InGaAs HEMT器件结构图;（b）器件结构的放大示意图

HEMT器件通常使用薄膜生长设备在衬底上生长多层半导体材料后，再经过多步工艺制备而成。图1展示了GaAs基InGaAs HEMT器件的基本结构。该结构由多个材料层构成，每一层都有其独特的功能。
[1] 衬底(substrate)：器件的底层材料，起到物理支撑、改善薄膜质量以及导热等作用。本案例衬底材料为GaAs，长度为5.2µm，厚度为0.6µm。
[2] 缓冲层(buffer)：用于缓解衬底与沟道层的晶格失配，保证沟道层的质量。本案例缓冲层材料为In_0.34Ga_0.33Al_0.33As，长度为5.2µm，厚度为0.6µm。
[3] 沟道层(channel)：二维电子气的传输通道。本案例沟道层材料为cx-In_0.53Ga_0.47As和cx-In_0.45Al_0.55As，长度为5.2µm，厚度为0.52µm。
[4] 隔离层(spacer)：阻止势垒层的电离杂质散射对沟道层的二维电子气造成影响。本案例隔离层材料为In_0.45Al_0.55As，长度为5.2µm，厚度为4nm。
[5] 掺杂层(dope)：二维电子气的电子提供层，具体的掺杂位置及浓度已在图1(b)中标出。 本案例中肖特基势垒层(barrier)材料为In_0.45Al_0.55As，重掺杂帽层(cap)材料为In_0.45Ga_0.55As。势垒层、掺杂层和隔离层均为宽禁带材料 InAlAs，它们和窄禁带的 InGaAs 沟道层形成异质结产生二维电子气。同时势垒层与栅金属形成肖特基接触，重掺杂帽层与源极和漏极金属形成欧姆接触。

二、物理模型设置

2.1 有源区载流子输运模型

$$\begin{array}{c}{\displaystyle R_{qw}=\frac{n-n_0}{\tau };\frac{1}{\tau }=\frac{1}{{\tau }_{300}}{e}^{(-\frac{T-300}{{\tau }_0})}}\\ {\displaystyle \frac{d{n}_t}{dt}=-\frac{n_t}{{\tau }_{\text{interb }}}+J_{\text{in }}+J_{out}-J_{fesc}}\\ {\displaystyle J_{fesc}=\frac{F_{\text{esc }}{n}_t{V}_{\text{fesc }}}{d};{\tau }_{\text{fesc }}=\frac{d}{V_{fesc}{F}_{\text{esc }}}}\end{array}\backslash begin\{gathered\}\; R\_\{q\; w\}=\backslash frac\{n-n\_0\}\{\backslash tau\}\; ;\; \backslash frac\{1\}\{\backslash tau\}=\backslash frac\{1\}\{\backslash tau\_\{300\}\}\; e^\{\backslash left(-\backslash frac\{T-300\}\{\backslash tau\_0\}\backslash right)\}\; \backslash \backslash \; \backslash frac\{d\; n\_t\}\{d\; t\}=-\backslash frac\{n\_t\}\{\backslash tau\_\{\backslash text\; \{interb\; \}\}\}+J\_\{\backslash text\; \{in\; \}\}+J\_\{o\; u\; t\}-J\_\{f\; e\; s\; c\}\; \backslash \backslash \; J\_\{f\; e\; s\; c\}=\backslash frac\{F\_\{\backslash text\; \{esc\; \}\}\; n\_t\; V\_\{\backslash text\; \{fesc\; \}\}\}\{d\}\; ;\; \backslash quad\; \backslash tau\_\{\backslash text\; \{fesc\; \}\}=\backslash frac\{d\}\{V\_\{f\; e\; s\; c\}\; F\_\{\backslash text\; \{esc\; \}\}\}\; \backslash end\{gathered\}$$

2.2 连续性方程

2.3 泊松方程 $$\begin{array}{c}{\displaystyle -\mathrm{\nabla }\cdot \left(\frac{{ϵ}_0{ϵ}_{dc}}{q}\mathrm{\nabla }V\right)=-n+p+N_D(1-f_D)-N_A{f}_A+\sum _j{N}_{tj}({\delta }_j-f_{tj})}\end{array}\backslash begin\{aligned\}\; -\backslash nabla\; \backslash cdot\backslash left(\backslash frac\{\backslash epsilon\_0\; \backslash epsilon\_\{d\; c\}\}\{q\}\; \backslash nabla\; V\backslash right)=-n+p+N\_D\backslash left(1-f\_D\backslash right)-N\_A\; f\_A+\backslash sum\_j\; N\_\{t\; j\}\backslash left(\backslash delta\_j-f\_\{t\; j\}\backslash right)\; \backslash end\{aligned\}$$

2.4 低场和高场迁移率模型

  低场迁移率模型 (Masetti Model)

$$\begin{array}{c}{\displaystyle {\mu }_0={\mu }_{\min 1}{e}^{-\frac{P_c}{N_i}}+\frac{{\mu }_{\max }{\left(\frac{T_L}{T_0}\right)}^{-\zeta }-{\mu }_{\min 2}}{1+{\left(\frac{N_i}{C_r}\right)}^{\alpha }}-\frac{{\mu }_1}{1+{\left(\frac{C_s}{N_i}\right)}^{\beta }}}\end{array}\backslash begin\{aligned\}\; \backslash mu\_0=\backslash mu\_\{\backslash min\; 1\}\; e^\{-\backslash frac\{P\_c\}\{N\_i\}\}+\backslash frac\{\backslash mu\_\{\backslash max\; \}\backslash left(\backslash frac\{T\_L\}\{T\_0\}\backslash right)^\{-\backslash zeta\}-\backslash mu\_\{\backslash min\; 2\}\}\{1+\backslash left(\backslash frac\{N\_i\}\{C\_r\}\backslash right)^\backslash alpha\}-\backslash frac\{\backslash mu\_1\}\{1+\backslash left(\backslash frac\{C\_s\}\{N\_i\}\backslash right)^\backslash beta\}\; \backslash end\{aligned\}$$

  高场迁移率模型 (Canali Model)

$$\begin{array}{c}{\displaystyle {\mu }_n=\frac{{\mu }_{0n}}{{(1+{\left({\mu }_{0n}F\mathrm{/}{v}_{sn}\right)}^{{\beta }_n})}^{1\mathrm{/}{\beta }_n}}}\\ {\displaystyle {\mu }_p=\frac{{\mu }_{0p}}{{(1+{\left({\mu }_{0p}F\mathrm{/}{v}_{sp}\right)}^{{\beta }_p})}^{1\mathrm{/}{\beta }_p}}}\end{array}\backslash begin\{aligned\}\; \backslash mu\_n=\backslash frac\{\backslash mu\_\{0\; n\}\}\{\backslash left(1+\backslash left(\backslash mu\_\{0\; n\}\; F\; /\; v\_\{s\; n\}\backslash right)^\{\backslash beta\_n\}\backslash right)^\{1\; /\; \backslash beta\_n\}\}\; \backslash \backslash \; \backslash mu\_p=\backslash frac\{\backslash mu\_\{0\; p\}\}\{\backslash left(1+\backslash left(\backslash mu\_\{0\; p\}\; F\; /\; v\_\{s\; p\}\backslash right)^\{\backslash beta\_p\}\backslash right)^\{1\; /\; \backslash beta\_p\}\}\; \backslash end\{aligned\}$$

2.5 碰撞电离模型 (Chynoweth Model)

$$\begin{array}{c}{\displaystyle {\alpha }_n={\alpha }_n^{\mathrm{\infty }}exp[-{\left(\frac{F_{cn}}{F}\right)}^{k_n}]}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_n=\backslash alpha\_n^\{\backslash infty\}\; exp\backslash left[-\backslash left(\backslash frac\{F\_\{c\; n\}\}\{F\}\backslash right)^\{k\_n\}\backslash right]\; \backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle {\alpha }_p={\alpha }_p^{\mathrm{\infty }}exp[-{\left(\frac{F_{Fp}}{F}\right)}^{k_p}]}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_p=\backslash alpha\_p^\{\backslash infty\}\; exp\backslash left[-\backslash left(\backslash frac\{F\_\{F\; p\}\}\{F\}\backslash right)^\{k\_p\}\backslash right]\; \backslash end\{aligned\}$$

2.6 隧穿模型 (Tunneling Model)

三、工作原理及结果讨论

3.1 材料特性

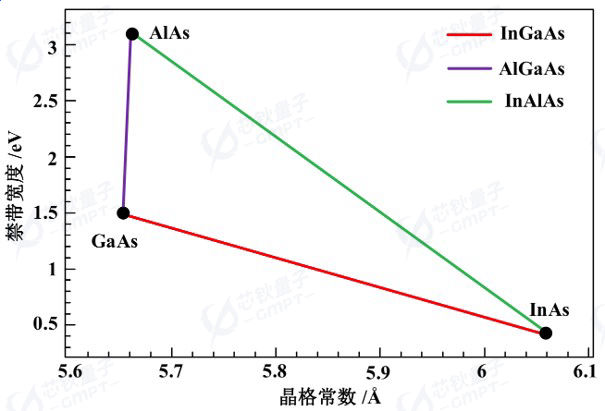
图2 InGaAlAs禁带宽度和晶格常数随组分的变化

InGaAs相比GaAs具有更高的载流子浓度和载流子迁移率，可以在高频和高功率应用中发挥更好的性能。此外，InGaAs材料的电子峰值速度比GaAs更高，具有良好的兼容性，可以与其他常见的III-V族半导体材料实现集成，大大拓展了器件的应用范围。InGaAlAs是一种四元化合物半导体材料，由InGaAs, AlGaAs或InAlAs以特定比例混合而成。通过改变In, Ga, Al的比例可以改变材料的晶格常数、禁带宽度（Eg）、电子迁移率（μ）和有效电子质量（mn*/m0）等[1]。如图2所示，随着In含量的增加，InGaAs的晶格常数增加，禁带宽度减少，电子迁移率获得提高。这些优势使得高In组分的InGaAs 作为沟道材料在高电子迁移率晶体管中受到关注。

3.2 能带分布

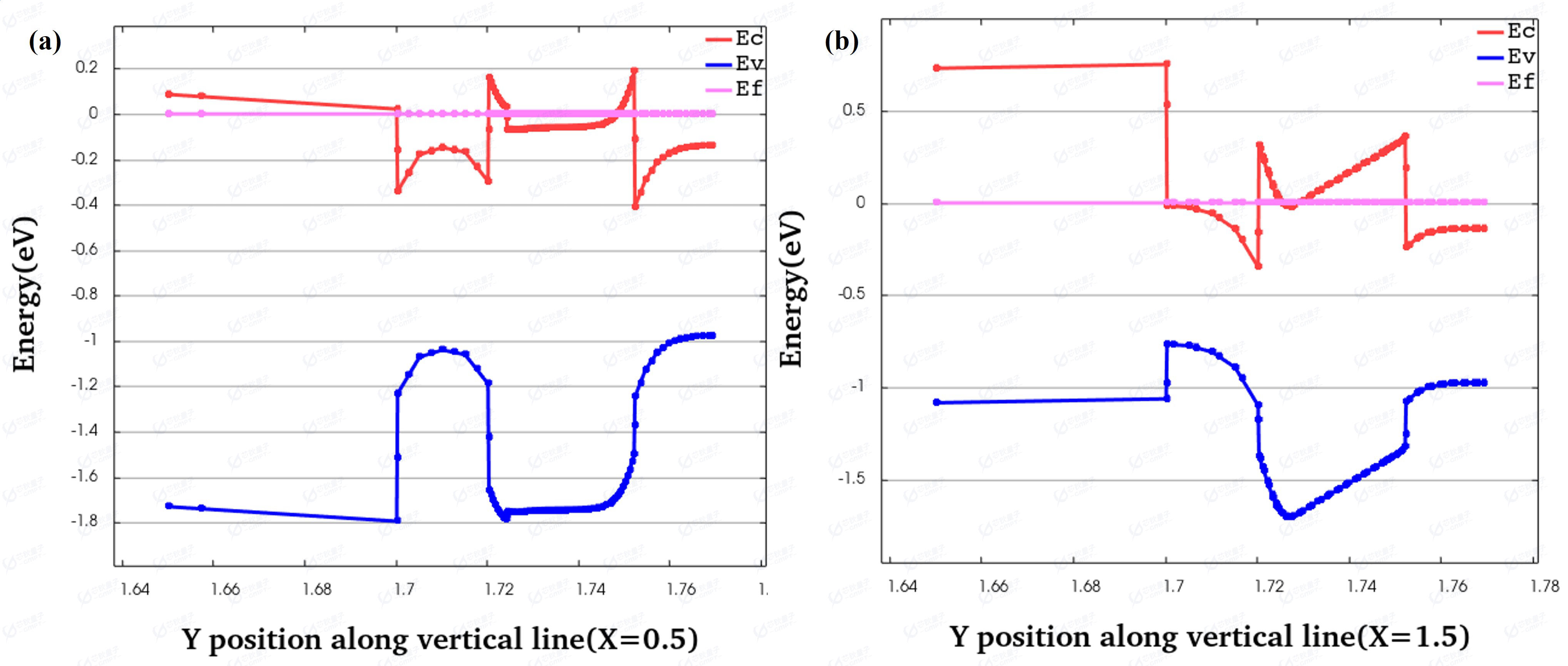
图3(a) (0.5,1.65)到(0.5,1.769)范围的能带图，图3(b) (1.5,1.65)到(1.5,1.769)范围的能带图。

图3(a)为器件从(0.5,1.65)到(0.5,1.769)范围内的能带图，图3(b)为器件从(1.5,1.65)到(1.5,1.769)范围内的能带图。通过图3(a)和(b)能带图的对比，不仅可以检验掺杂设置的正确性，还可以查看电子和空穴浓度分布以及二维电子气分布。可以看出，X=1.5µm位置处的电子浓度明显低于X=0.5µm位置处，因n掺杂导致的导带价带变化以及InGaAs 和InAlAs 两种材料界面形成的二维电子气分布在图3均一一对应。

3.3 二维电子气

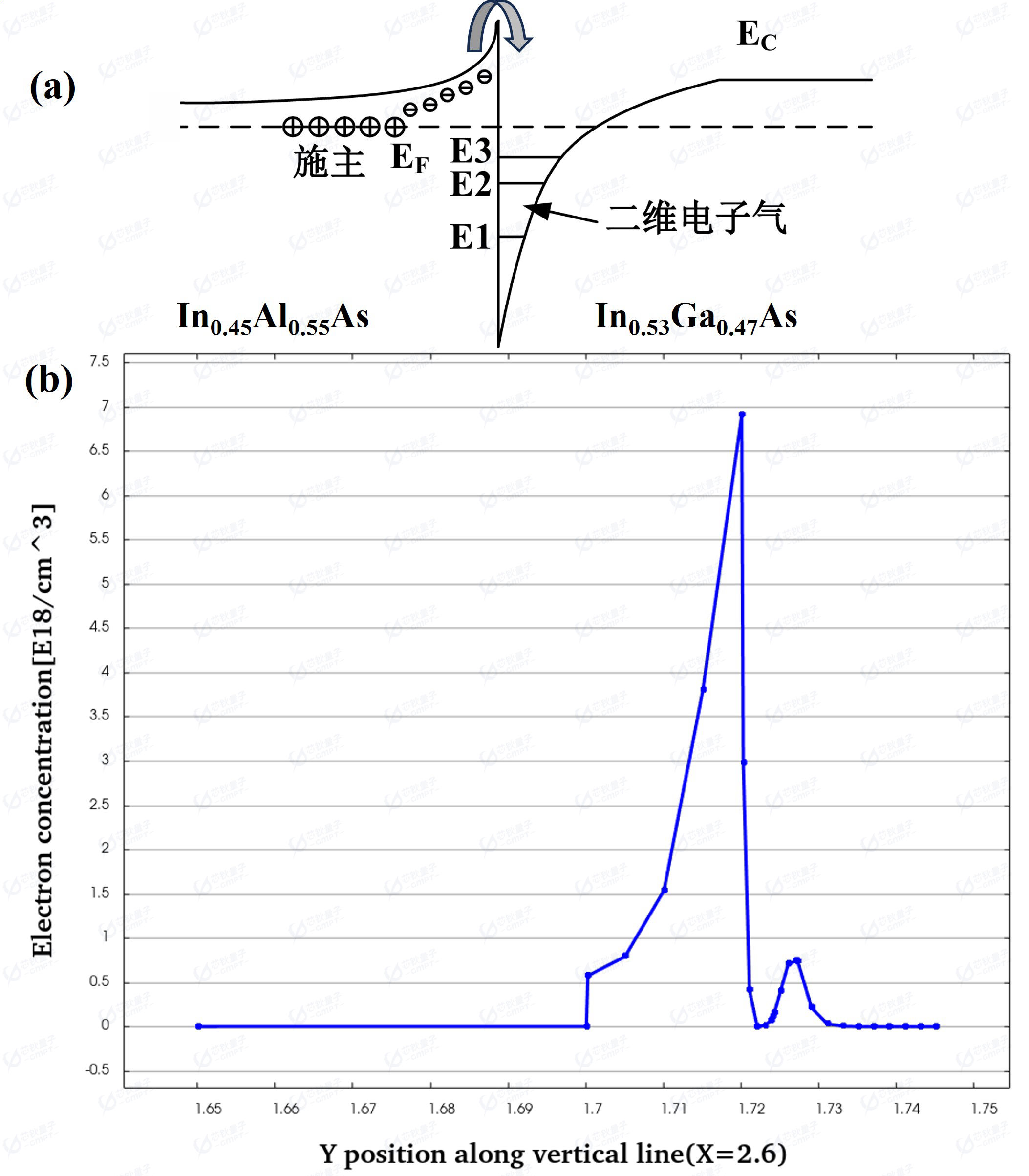
图4 (a)二维电子气原理图 (b)器件从(2.6,1.65)到(2.6,1.745)范围内的电子浓度分布图

n掺杂的宽禁带材料InAlAs和未掺杂的窄禁带材料InGaAs的费米能级存在显著差异，形成异质结后费米能级重新排列导致电子从InAlAs转移到InGaAs，如图4(a)所示。这个过程会在InAlAs一侧形成耗尽区，留下空间固定正电荷，使得能带弯曲形成势垒；在InGaAs一侧形成势阱，电子按顺序占据可用的最低能量状态，使得势阱积累了n掺杂的InAlAs分离的电子，被限制在势阱内的电子只有平行于界面的二维自由度，称为二维电子气。如图4(b)所示，形成的二维电子气均在Y=1.72µm处的In_0.53Ga_0.47As积累。势阱中积累的电子由掺杂的In_0.45Al_0.55As 提供，但是位于非掺杂的In_0.53Ga_0.47As沟道层中，因此受益于非掺杂层的电子传输特性，拥有很高的电子迁移率[2]。这种掺杂技术被称为调制掺杂，与传统掺杂相比可以同时实现高载流子浓度和高电子迁移率。

3.4 栅极开关

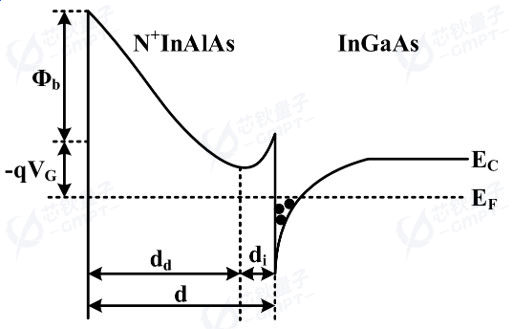
图5 栅极开关特性

常规的HEMT为耗尽型器件，其工作原理同样是通过向栅极施加偏压形成电场来控制沟道中二维电子气的浓度，施加负偏压就是消耗二维电子气浓度直到沟道关闭，施加正偏压就是增加二维电子气浓度直到达到饱和。栅极偏压对沟道二维电子气的调控如图5所示，Фb为肖特基势垒的高度，VG为栅极施加的偏置电压，dd为掺杂的 InAlAs 势垒层厚度，di为未掺杂的 InAlAs 阻挡层厚度，d为宽禁带材料InAlAs的厚度。而该结构通过减薄栅极下方的势垒层的厚度抬高导带以逐步耗尽栅极下方沟道中二维电子气，从而实现增强型。

3.5 输出特性和转移特性

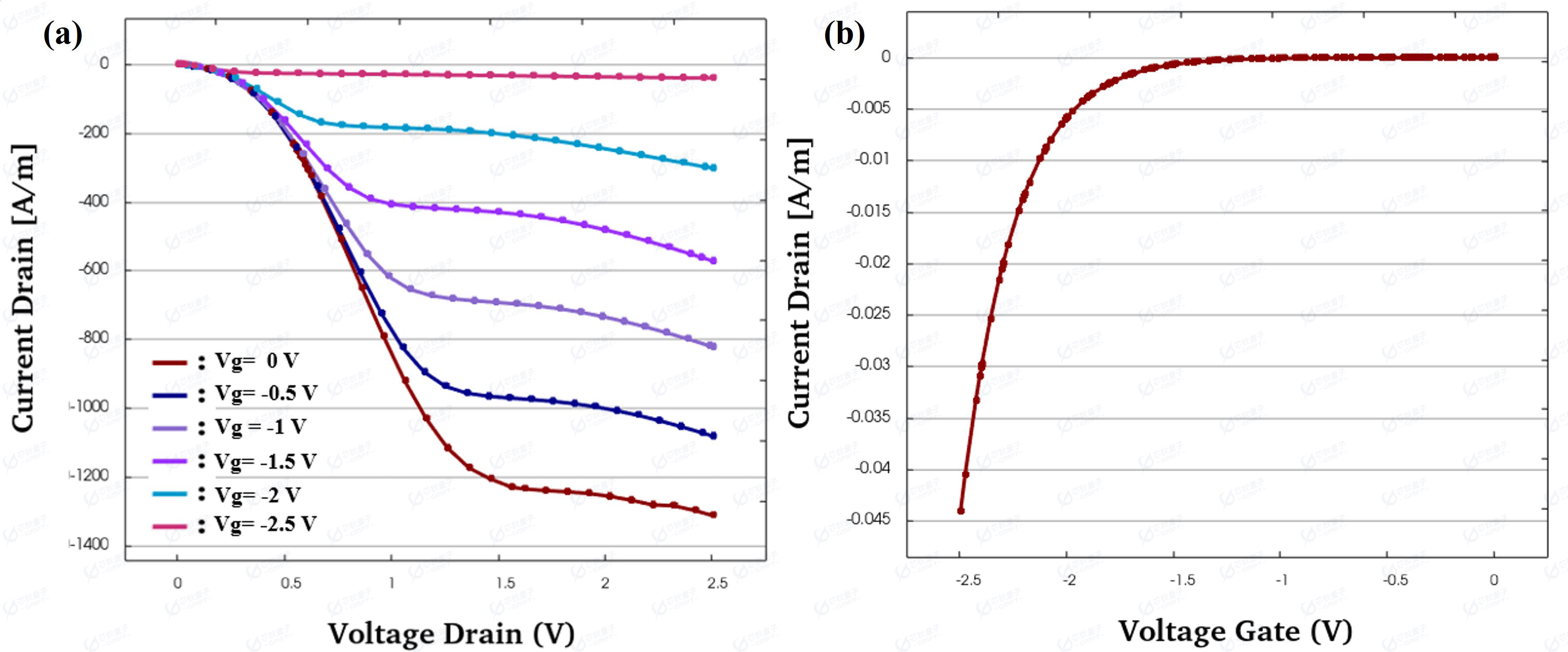
图6 (a)输出特性曲线 (b)转移特性曲线

图6(a)为栅极电压分别为0V,-0.5V,-1V,-1.5V,-2V和-2.5V时漏极电压和漏极电流的输出特性曲线。图6(b)为转移特性曲线，当栅极电压为0时，器件未开启，该器件类型为增强型。HEMT的输出特性曲线同样分为线性区、饱和区和截止区，反映了二维电子气的分布与调控机制。当Vd较低时，沟道未夹断，电流受沟道电阻主导。此时，电子在二维电子气形成的沟道中高速迁移，电流随Vd线性增长。当Vd增大至夹断电压时，漏极端电场增强，沟道逐渐夹断，二维电子气被限制在源极附近狭窄区域。此时，电流大小由Vg控制的二维电子气浓度决定。图6(a)中可以看出器件进入饱和区后，主要受Vg控制，基本不受Vd影响。此外，随着Vg负向偏置的增加，二维电子气逐渐被耗尽，沟道电阻变大导致电流随之迅速减小。最终二维电子气被完全耗尽，器件进入截止区。

四、总结

本案例通过Nuwa TCAD半导体仿真软件对 InGaAs HEMT 进行建模与仿真，深入探讨了器件的工作原理、结构组成、物理模型及其伏安特性，仿真结果与理论相符。对于 InGaAs HEMT 这种复杂的高电子迁移率晶体管器件，Nuwa TCAD能够帮助设计者预测器件的性能、优化器件设计参数、深入了解其工作原理以及探索新的材料组合以进一步提升器件性能。

参考文献

[1] 金东东，Ⅲ-Ⅴ族半导体异质结二维电子气输运特性研究，清华大学博士论文
[2] 康东旭，高In组分GaAs基InGaAs MHEMT研究 ，桂林电子科技大学硕士论文