使用Nuwa TCAD软件仿真和设计SiC SBD器件

GMPT, 2024/05/17

摘要： 碳化硅（SiC）半导体材料是目前电力电子领域发展最快的半导体材料之一。其中4H-SiC由于其较宽的能带间隙（约3.2 eV）、较高的击穿电压以及优秀的电子迁移率，在高功率、高频率的电子器件应用中展现出卓越性能。

   SiC半导体功率器件主要包括两大类：二级管类和晶体管类，其中SiC肖特基势垒二极管（SiC SBD），具有高反向恢复速度、高耐压、高频等特点，广泛应用于空调、电源、光伏发电系统中的功率调节器、电动汽车的快速充电器等的功率因数校正电路（PFC电路）和整流桥电路中。本文将基于Nuwa TCAD软件对4H-SiC 基的SBD进行相关仿真和设计，并展示软件仿真结果。

一、器件结构

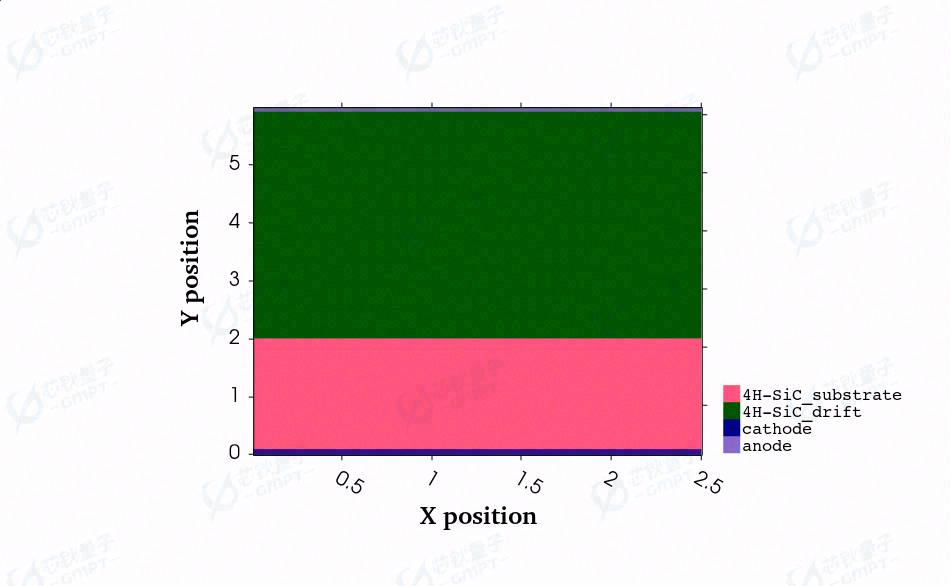
图1. SiC SBD器件结构示意图

   在此项工作中，4H-SiC基SBD器件结构设计如图1所示。其中，漂移区厚度设置为4$\mu \backslash mu$m，掺杂水平设置在$1\times 10^{16}{cm}^{-3}1\backslash times\; 10^\{16\}\; \{cm\}^\{-3\}$，重掺杂衬底区厚度设置为2$\mu \backslash mu$m，掺杂水平设置在$5\times 10^{19}{cm}^{-3}5\backslash times\; 10^\{19\}\; \{cm\}^\{-3\}$，器件整体宽度设定为2.5$\mu \backslash mu$m，阳极肖特基功函数设定为5.15 eV。

二、物理模型设置

2.1 热电子发射模型

2.2 连续性方程

$$\begin{array}{cccc}& {\displaystyle \mathrm{\nabla }\cdot J_n-\sum _j{R}_n^{tj}-R_{sp}-R_{st}-R_{au}+G_{opt}(t)=\frac{\mathrm{\partial }n}{\mathrm{\partial }t}+N_D\frac{\mathrm{\partial }{f}_D}{\mathrm{\partial }t}}& & \end{array}\backslash begin\{align\}\; \backslash nabla\; \backslash cdot\; J\_n-\backslash sum\_j\; R\_n^\{t\; j\}-R\_\{s\; p\}-R\_\{s\; t\}-R\_\{a\; u\}+G\_\{o\; p\; t\}(t)=\backslash frac\{\backslash partial\; n\}\{\backslash partial\; t\}+N\_D\; \backslash frac\{\backslash partial\; f\_D\}\{\backslash partial\; t\}\; \backslash end\{align\}$$ $$\begin{array}{cccc}& {\displaystyle \mathrm{\nabla }\cdot J_p+\sum _j{R}_p^{tj}+R_{sp}+R_{st}+R_{au}-G_{opt}(t)=-\frac{\mathrm{\partial }p}{\mathrm{\partial }t}+N_A\frac{\mathrm{\partial }{f}_A}{\mathrm{\partial }t}}& & \end{array}\backslash begin\{align\}\; \backslash nabla\; \backslash cdot\; J\_p+\backslash sum\_j\; R\_p^\{t\; j\}+R\_\{s\; p\}+R\_\{s\; t\}+R\_\{a\; u\}-G\_\{o\; p\; t\}(t)=-\backslash frac\{\backslash partial\; p\}\{\backslash partial\; t\}+N\_A\; \backslash frac\{\backslash partial\; f\_A\}\{\backslash partial\; t\}\; \backslash end\{align\}$$

2.3 泊松方程

$$-\mathrm{\nabla }\cdot \left(\frac{{ϵ}_0{ϵ}_{dc}}{q}\mathrm{\nabla }V\right)=-n+p+N_D(1-f_D)-N_A{f}_A+\sum _j{N}_{tj}({\delta }_j-f_{tj})-\backslash nabla\; \backslash cdot\backslash left(\backslash frac\{\backslash epsilon\_0\; \backslash epsilon\_\{d\; c\}\}\{q\}\; \backslash nabla\; V\backslash right)=-n+p+N\_D\backslash left(1-f\_D\backslash right)-N\_A\; f\_A+\backslash sum\_j\; N\_\{t\; j\}\backslash left(\backslash delta\_j-f\_\{t\; j\}\backslash right)$$

2.4 低场和高场迁移率模型

低场迁移率模型

高场迁移率模型(Canali Model)

2.5 界面缺陷模型 Exponential tail Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{E_{tail}}{e}^{[-\frac{(E-E_0)}{E_{tail}}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{E\_\{\; \{tail\; \}\}\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)\}\{E\_\{\{tail\; \}\}\}\backslash right]\}$$

Gaussian Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.6 体缺陷模型 Shockley-Read-Hall Model

$$\begin{array}{c}{\displaystyle R_n^{tj}=c_{nj}n{N}_{tj}(1-f_{tj})-c_{nj}{n}_{1j}{N}_{tj}{f}_{tj}}\end{array}\backslash begin\{aligned\}R\_n^\{t\; j\}=c\_\{n\; j\}\; n\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)-c\_\{n\; j\}\; n\_\{1\; j\}\; N\_\{t\; j\}\; f\_\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle R_p^{tj}=c_{pj}p{N}_{tj}{f}_{tj}-c_{pj}{p}_{1j}{N}_{tj}(1-f_{tj})}\end{array}\backslash begin\{aligned\}R\_p^\{t\; j\}=c\_\{p\; j\}\; p\; N\_\{t\; j\}\; f\_\{t\; j\}-c\_\{p\; j\}\; p\_\{1\; j\}\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle N_{tj}\frac{\mathrm{\partial }{f}_{tj}}{\mathrm{\partial }t}=R_n^{tj}-R_p^{tj}}\end{array}\backslash begin\{aligned\}N\_\{t\; j\}\; \backslash frac\{\backslash partial\; f\_\{t\; j\}\}\{\backslash partial\; t\}=R\_n^\{t\; j\}-R\_p^\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle c_{nj}={\sigma }_{nj}{v}_n={\sigma }_{nj}\sqrt{\frac{8kT}{\pi m_n}};c_{pj}={\sigma }_{pj}{v}_p={\sigma }_{pj}\sqrt{\frac{8kT}{\pi m_p}}}\end{array}\backslash begin\{aligned\}c\_\{n\; j\}=\backslash sigma\_\{n\; j\}\; v\_n=\backslash sigma\_\{n\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_n\}\}\; ;\; \backslash quad\; c\_\{p\; j\}=\backslash sigma\_\{p\; j\}\; v\_p=\backslash sigma\_\{p\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_p\}\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle \frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj};\frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj}}\end{array}\backslash begin\{aligned\}\backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\};\; \backslash quad\; \backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\}\backslash end\{aligned\}$$

Gaussian Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.7 碰撞电离模型 Chynoweth Model

$$\begin{array}{c}{\displaystyle {\alpha }_n={\alpha }_n^{\mathrm{\infty }}{e}^{-{\left(\frac{F_{cn}}{F}\right)}^{{\kappa }_n}}}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_n=\backslash alpha\_n^\{\backslash infty\}\; e^\{-\backslash left(\backslash frac\{F\_\{c\; n\}\}\{F\}\backslash right)^\{\backslash kappa\_n\}\}\; \backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle {\alpha }_p={\alpha }_p^{\mathrm{\infty }}{e}^{-{\left(\frac{{}_{cp}}{F}\right)}^{{\kappa }_p}}}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_p=\backslash alpha\_p^\{\backslash infty\}\; e^\{-\backslash left(\backslash frac\{\{\; \}\_\{c\; p\}\}\{F\}\backslash right)^\{\backslash kappa\_p\}\}\; \backslash end\{aligned\}$$

碰撞电离参数设置

	${\alpha }^{\mathrm{\infty }}(1\mathrm{/}m)\backslash alpha^\{\backslash infty\}(1\; /\; m)$	$F_{\mathrm{c}}(V\mathrm{/}m)F\_\{\backslash mathrm\{c\}\}(V\; /\; m)$	$\kappa \backslash kappa$	Feild range to $(\mathrm{V}\mathrm{/}\mathrm{m})(\backslash mathrm\{V\}\; /\; \backslash mathrm\{m\})$
Electron	$2\times 10^{10}2\; \backslash times\; 10^\{10\}$	$3.6\times 10^{10}3.6\; \backslash times\; 10^\{10\}$	1	$\mathrm{\infty }\backslash infty$
Hole	$1.34\times 10^{10}1.34\; \backslash times\; 10^\{10\}$	$2.03\times 10^{9}2.03\; \backslash times\; 10^\{9\}$	1	$\mathrm{\infty }\backslash infty$

三、结果与讨论

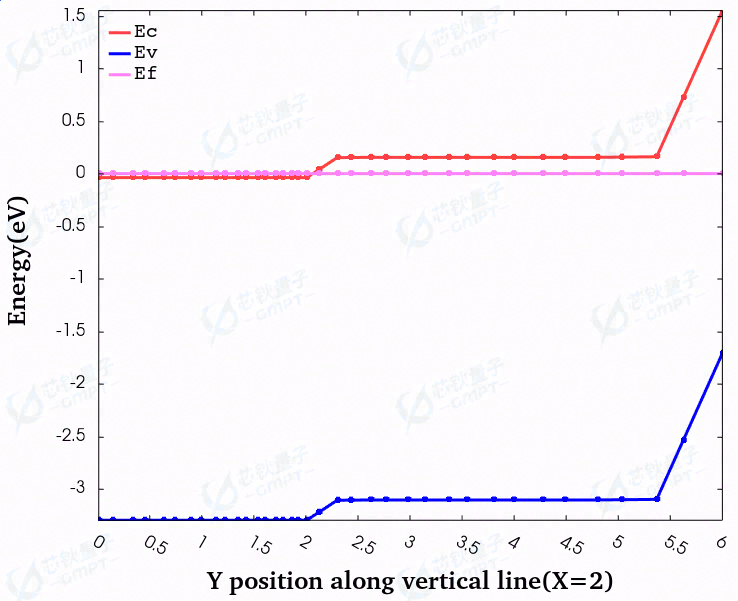
图2. 器件纵切能带图

   在此项工作中，截取器件纵向能带分布，如图2所示。X轴起始点为阴极接触面。相比于实验值1.55 eV，器件表面肖特基接触势垒观测值为1.548 eV，与实验值基本相符。另外，在漂移层与衬底界面附近，存在一个由于浓度差异造成的很小的势垒，其势垒大小为0.191 eV（漂移扩散过程形成的）。

3.1 正向输出特性

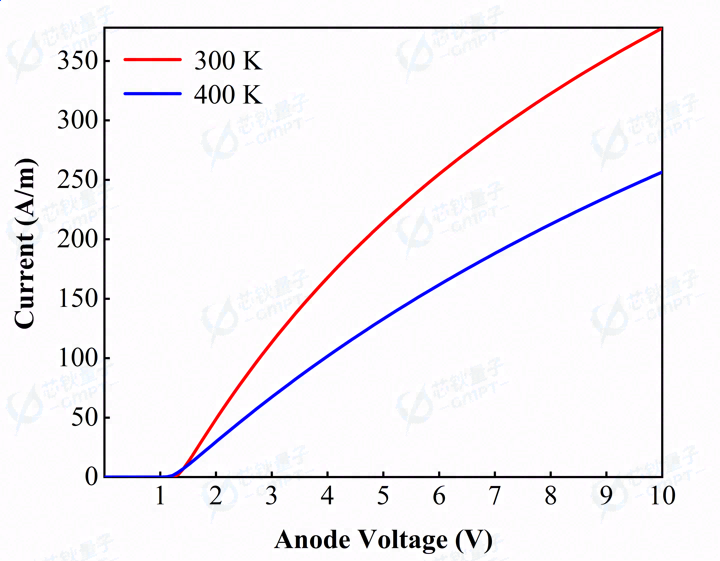
图3. 器件正向I-V特性曲线

   在本工作中，器件掺杂为n型，器件导通时以电子电流为主，器件整体电流几乎全为电子电流贡献，空穴电流水平几乎为零，空穴基本不参与输运过程，器件本身为单极型器件。观察图3，300 K温度条件下，二极管的开启电压为1.221 V（I=0.113 A/m），电压为10 V时，器件的电流面密度约为377 A/m；当温度提升至400 K时，二极管的开启电压为1.121 V（I=0.187 A/m），电压为10 V时，器件的电流面密度约为257 A/m。

   在器件正向工作时，当器件外置正向偏置小于开启电压，由于温度升高,带来更强的热电子发射过程，所以器件开启电压随温度升高而减小。

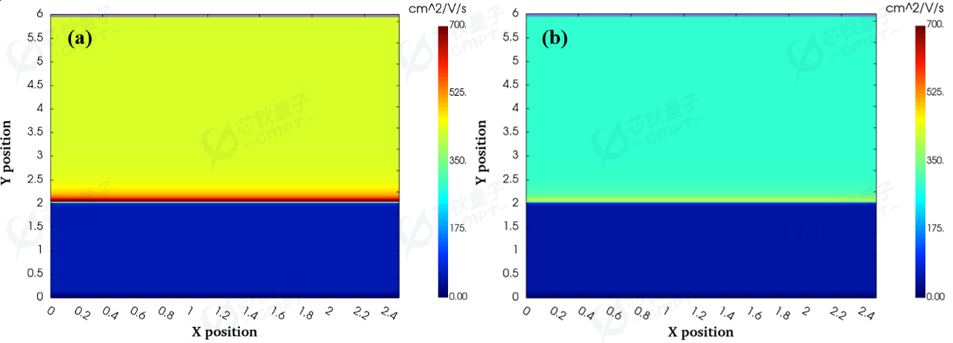
图4. 温度为（a）300 K和（b）400 K的二维电子迁移率分布

   当器件导通后，外部载流子注入，由于300 K到400 K阶段，杂质已经全部电离，而本征激发可以忽略，载流子浓度不随温度变化，因此晶格振动散射成为主要矛盾，温度的升高增强了晶格振动散射概率，导致载流子平均自由时间减小，如公式（1）所示

$$\begin{array}{cccc}& {\tau }_s\propto T^{-3\mathrm{/}2}& & \text{(1)}\end{array}\backslash tau\_s\; \backslash propto\; T^\{-3\; /\; 2\}\backslash tag\{1\}$$

由公式（2）可知，载流子迁移率随温度的上升而下降（如图4所示），进而造成器件到达开启电压后的正向电流密度J减小。如公式（3）和公式（4）所示

$$\begin{array}{cccc}& J=\sigma \mathrm{\mid }E\mathrm{\mid }& & \text{(4)}\end{array}J=\backslash sigma|E|\backslash tag\{4\}$$

3.2 反向阻断特性

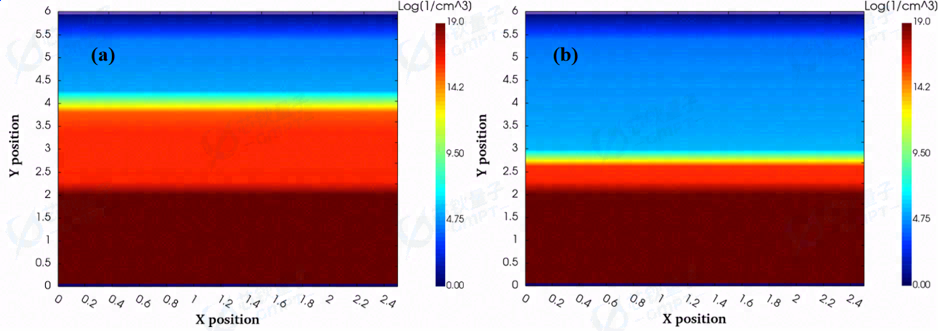
图5. 器件反向偏置电压为（a）50 V和（b）100V的载流子浓度分布

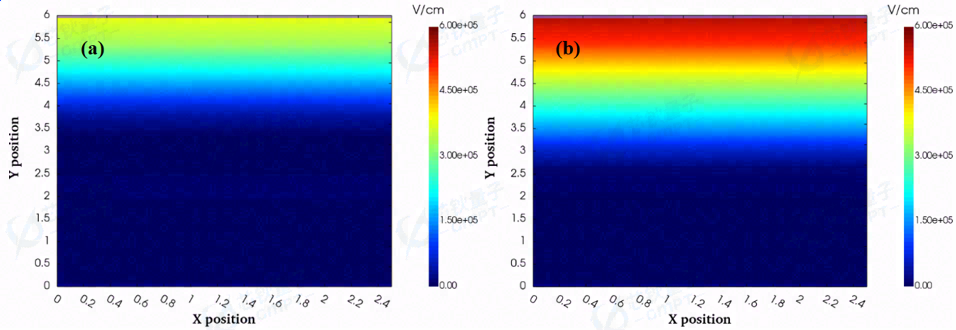
图6. 器件反向偏置电压为（a）50 V和（b）100V的场强分布

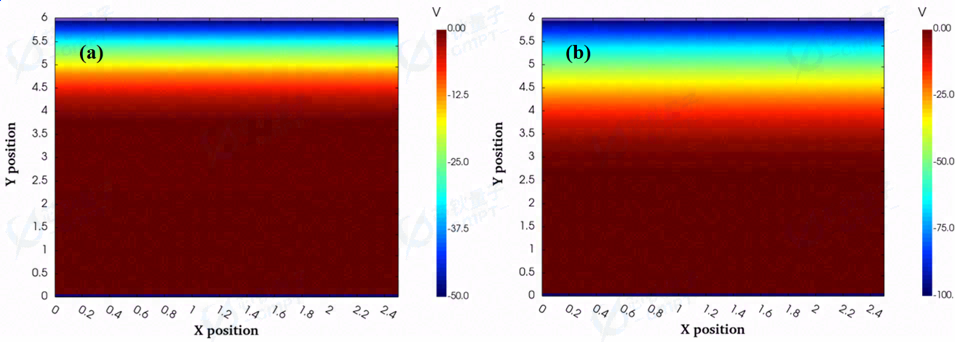
图7. 器件反向偏置电压为（a）50 V和（b）100V的电势分布

   50 V和100 V情况下的载流子浓度、电场、电势分布图如图5、图6、图7所示。当器件呈反向偏置状态时，耗尽区作为承载场强的主要区域，受反向电压影响，表面肖特基接触形成的耗尽区不断扩大，电子被不断耗尽，电势与耗尽区承担场强不断上升且向器件内部延伸。

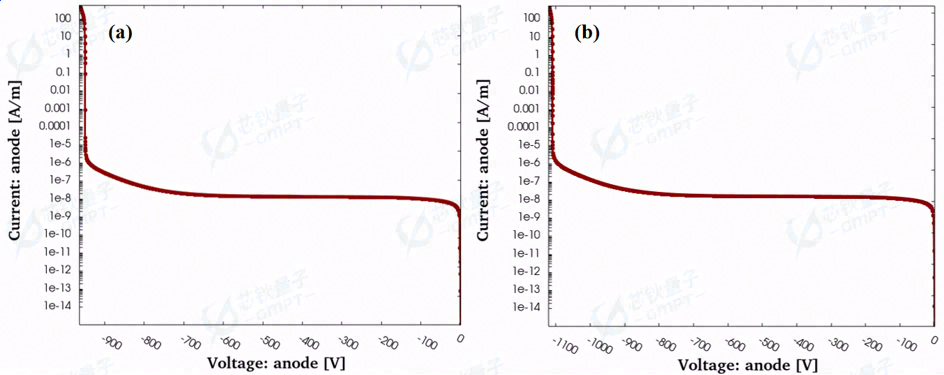
图8. 温度为（a）300 K和（b）400 K的反向击穿曲线

   在此次仿真工作中，同样计算并分析不同温度（300 K和400 K）下的器件关态特性，反向击穿曲线如图8所示。根据前面提到碰撞电离模型，本工作中设计的器件的击穿电压在940 V附近，当温度提升至400 K时，器件的击穿电压在1110 V附近。

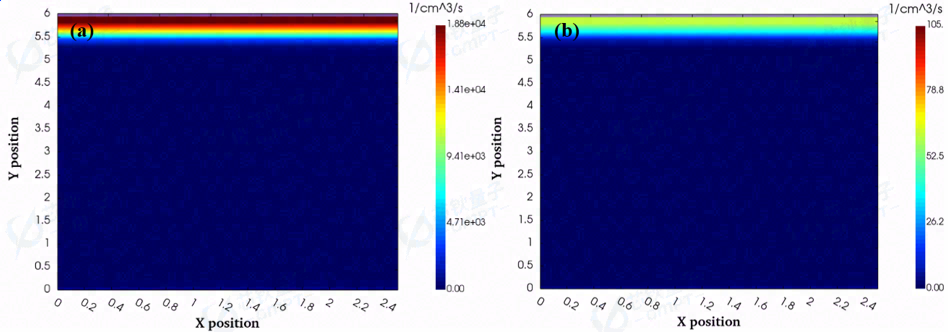
图9. 反向偏置100V器件在（a）300 K和（b）400 K温度下的碰撞电离率二维分布

   由于温度提高导致的本征载流子浓度提高，器件内部的迁移率下降，影响了碰撞电离过程中的平均自由程，导致碰撞电离几率下降（如图9所示），器件击穿电压升高。

3.3 电容-频率特性

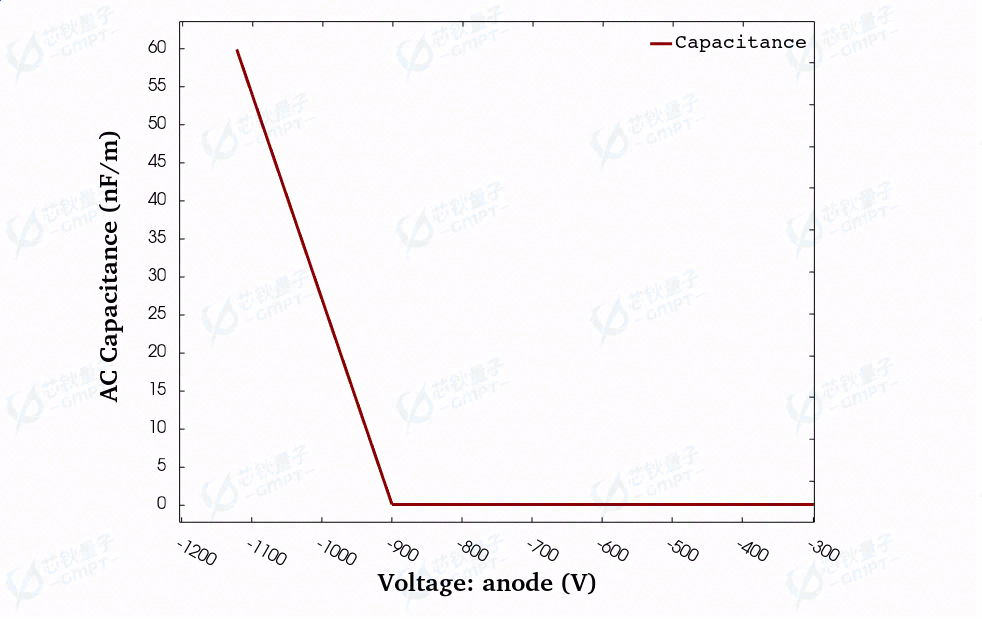
图10. 器件反向C-V特性曲线

   图10展示了器件处于关态时的C-V特性曲线，在器件尚未击穿时，器件不断被耗尽，器件本身电荷不会增加，当接近击穿电压时（900 V以上），由于碰撞电离率不断上升，器件内部电荷不断增加，从而出现电容随着电压增大而不断增大的现象。

3.4 反向恢复特性

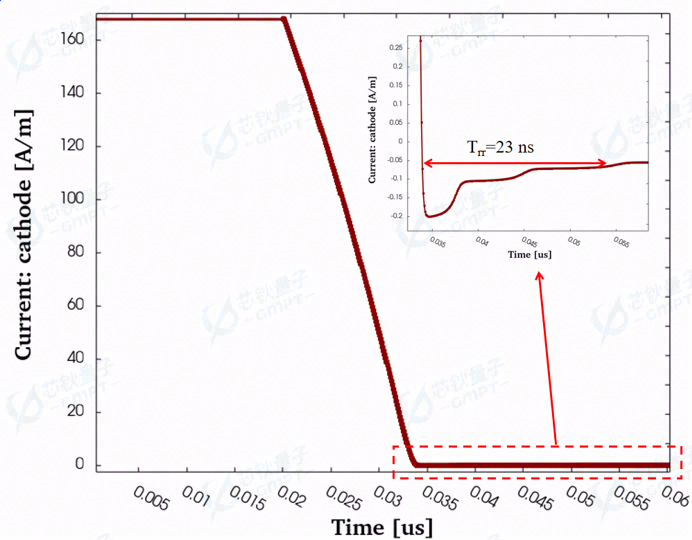
图11. 反向恢复特性曲线

   对于当前功率电子应用市场，SiC SBD器件主要应用于高频，高功率环境中，因此在高速的开关过程中，优异的反向恢复特性可以减小器件功耗，提高开关频率。本项工作研究了SiC SBD器件的反向恢复特性，如图11所示。观测仿真数据可知，SiC SBD展现了优异的反向恢复电流和反向恢复时间，其中反向恢复时间仅为23 ns。

四、总结

   本文对SiC SBD器件进行了仿真和设计，介绍了仿真中引用的物理模型的公式和参数，并展示了器件的仿真结果，包括能带图、正向输出特性、反向阻断特性、电容-频率特性和反向恢复特性。通过Nuwa TCAD软件得到的仿真结果，本文进一步分析了器件内部机理，包括能带分布、载流子迁移和晶格振动等，为SiC SBD器件结构分析和器件性能提升提供了思路。