使用Nuwa TCAD软件仿真提升超结VDMOS器件(含终端)的击穿电压
GMPT, 2024/06/07
摘要: 超结垂直双扩散金属氧化物半导体(Superjunction Vertical Double-Diffused Metal Oxide Semiconductor, 超结VDMOS)场效应晶体管,作为一种功率器件,由于其既有普通MOS开关速度快、静态输入阻抗高,又有双极晶体管电流能力强的优点,被广泛应用于电机调速、雷达、马达驱动、逆变器、不间断电源、开关电源、高保真音响、汽车电子、移动通信、节能灯和电子镇流器等诸多领域。由于在器件边缘处会出现电场集中效应,这使得器件无法充分发挥材料临界击穿电场高的优点,这就需要通过设计合适的终端结构来改善,提升器件的反向击穿电压。
本文研究了一种电荷不平衡的超结VDMOS终端结构[1],并使用Nuwa TCAD软件对该终端结构进行仿真,验证了电荷不平衡终端结构击穿电压高于电荷平衡终端结构击穿电压的结论。
一、超结VDMOS器件
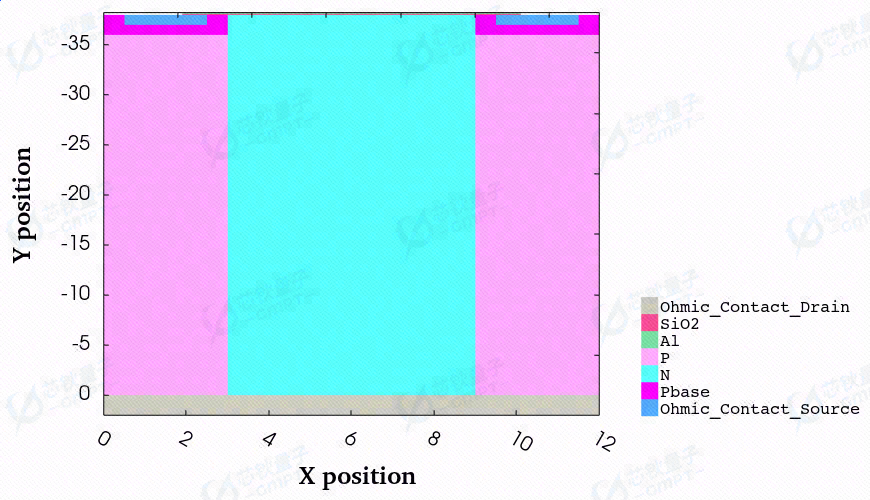
图1. 超结VDMOS器件结构示意图
超结VDMOS器件如图所示,其I-V特性与普通MOS基本相同。
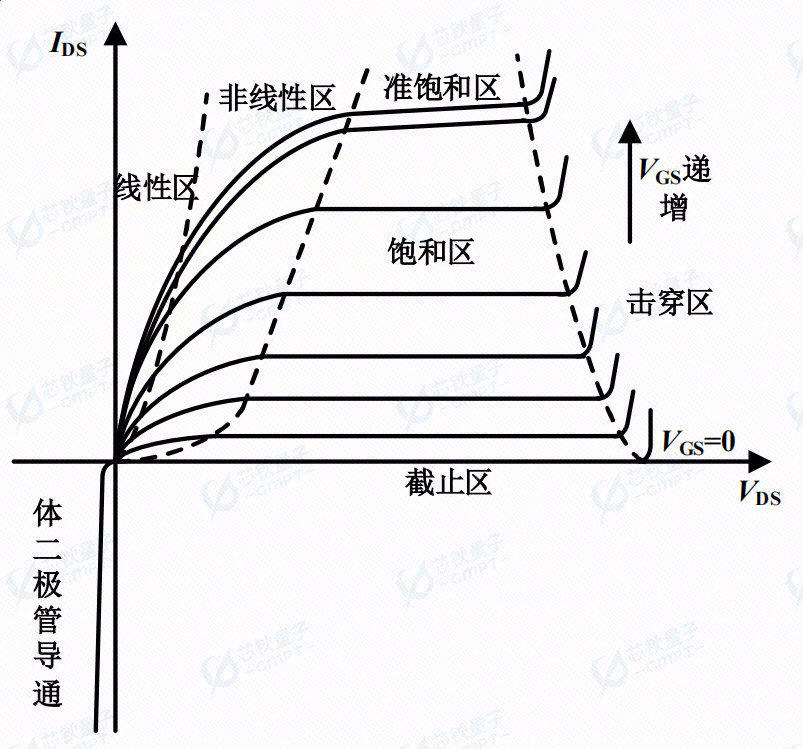
图2. 超结VDMOS器件的I-V特性
如图2所示,当栅极未加电压或栅极电压未超过器件的阈值电压V t h V t h I D S I D S V G S > V t h V GS > V t h V D S V D S V G S > V t h V GS > V t h V D S V D S V G S − V t h V GS − V t h V D S V D S V D S > ( V G S − V t h ) V D S > ( V GS − V t h ) I D S I D S V D S V D S I D S I D S V D S V D S V G S V GS V D S V D S I D S I D S
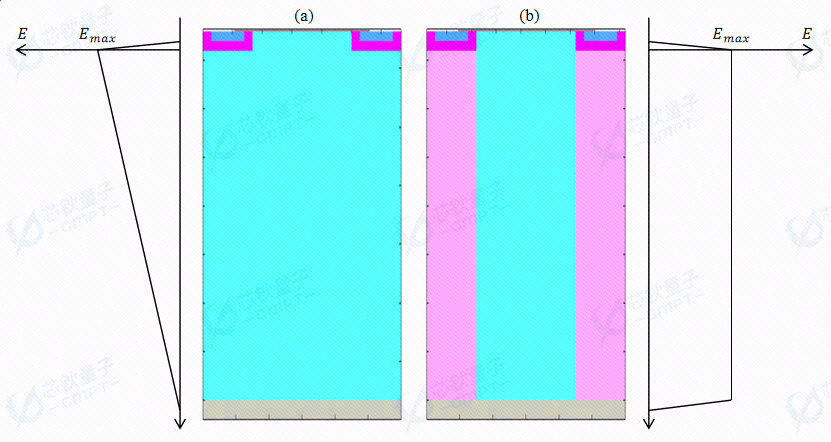
图3. (a)普通VDMOS器件的电场曲线 (b)超结VDMOS器件的电场曲线
图3展示了普通VDMOS器件和超结VDMOS器件的电场曲线。超结VDMOS在普通VDMOS结构的基础上引入了超结结构,代替了原漂移区的轻掺杂结构,使得器件处于反偏状态时,在横向电场的作用下N型半导体与P型半导体的电荷相互补偿耗尽,对外不表现出电性,超结区域形成横向耐压层。从正电荷出发的电场线遇到的都是成对的正负电荷,它们极性相反相互抵消,因此找不到能够终止的负电荷,于是只好穿过超结区域。这就使得耗尽区域内的电场强度变化不大,电场曲线的面积相较于普通VDMOS器件的电场曲线而言大大增加,这意味着器件的击穿电压得到巨大提高。
二、超结终端
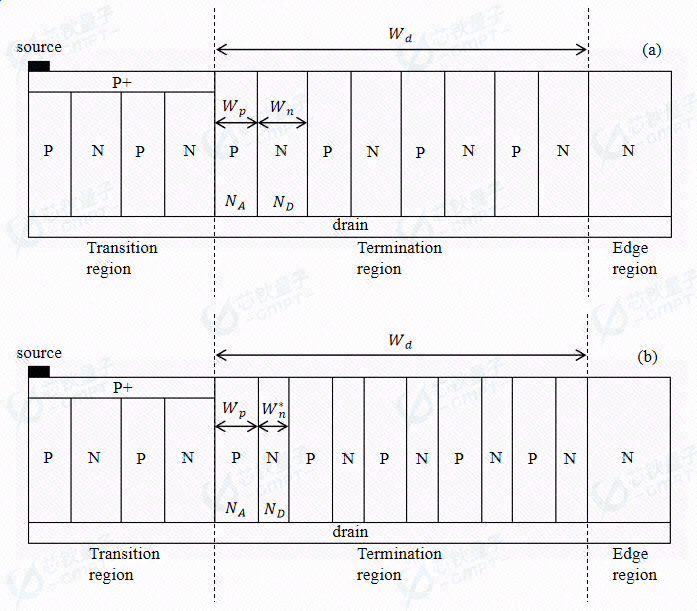
常用的终端技术有场限环、场板、结终端扩展、横向变掺杂以及RESURF技术等,本文将研究如下图所示的电荷平衡和电荷不平衡的超结终端。
图4. (a)电荷平衡终端结构示意图 (b)电荷不平衡终端结构示意图
电荷平衡条件为
Q n = Q p Q n = Q p
应用到终端结构中的P、N柱之后可写为
N A W p = N D W n N A W p = N D W n 图4中的电荷平衡终端满足上述条件,电荷不平衡终端将N柱宽度W n W n W n ∗ W n ∗ N A W p > N D W n ∗ N A W p > N D W n ∗
电荷平衡终端
首先计算电荷平衡终端的击穿电压
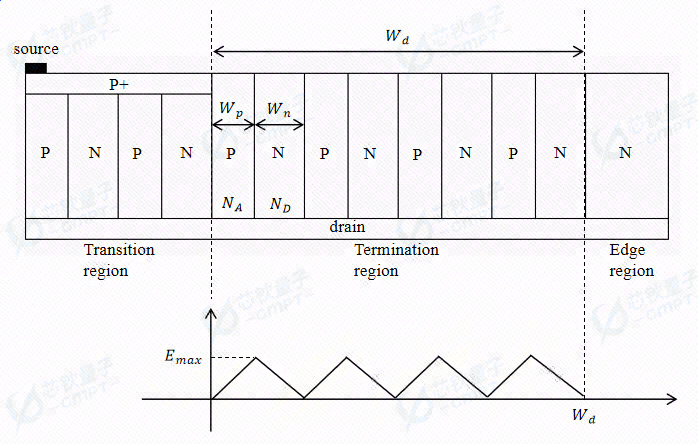
图5. 电荷平衡终端结构及其电场曲线
此时器件电荷平衡,PN结完全耗尽,在PN结表面的电场强度最大
E m a x = q N A W p ϵ = q N D W n ϵ E ma x = ϵ q N A W p = ϵ q N D W n
此时器件击穿电压即为电场强度曲线的面积
B V b a l a n c e = 1 2 W d E m a x = 1 2 W d q N A W p ϵ = 1 2 W d q N D W n ϵ B V ba l an ce = 2 1 W d E ma x = 2 1 W d ϵ q N A W p = 2 1 W d ϵ q N D W n
电荷不平衡终端
由参考文献[2][3]可知,电荷不平衡终端的击穿电压可分为两部分计算,第一部分是分别计算终端区每个PN结耗尽区域的击穿电压,第二部分是将整个终端区等效地视作一个P型半导体计算其击穿电压(由于P柱电荷未完全耗尽),电荷不平衡终端的击穿电压为两部分计算结果之和。
首先计算第一部分
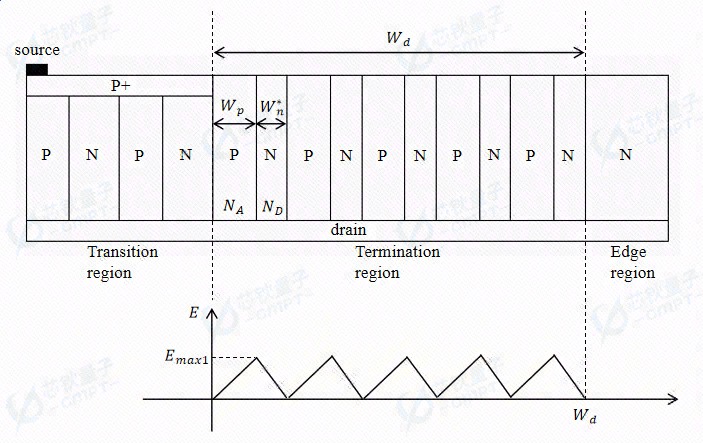
图6. 电荷不平衡终端结构(第一部分)及其电场曲线
此时N柱电荷已耗尽,与电荷平衡情况同理,可由N柱参数计算击穿电压
B V 1 = 1 2 W d E m a x 1 = 1 2 W d q N D W n ∗ ϵ B V 1 = 2 1 W d E ma x 1 = 2 1 W d ϵ q N D W n ∗
接下来计算第二部分
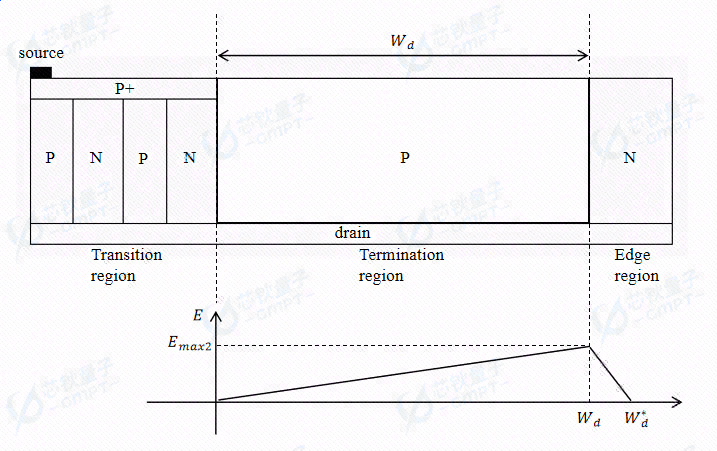
图7. 电荷不平衡终端结构(第二部分)及其电场曲线
由于P柱电荷并未完全耗尽,所以可将终端区等效地视作P型半导体。电荷不平衡终端中单个PN结的剩余电荷为
N A W p − N D W n ∗ N A W p − N D W n ∗ W d W p + W n ∗ W p + W n ∗ W d Q = ( N A W p − N D W n ∗ ) W d W p + W n ∗ Q = ( N A W p − N D W n ∗ ) W p + W n ∗ W d E m a x 2 = q Q ϵ = q ( N A W p − N D W n ∗ ) W d ϵ ( W p + W n ∗ ) E ma x 2 = ϵ qQ = ϵ ( W p + W n ∗ ) q ( N A W p − N D W n ∗ ) W d δ W d = W d ∗ − W d = Q N D = N A W p − N D W n ∗ N D W d W p + W n ∗ δ W d = W d ∗ − W d = N D Q = N D N A W p − N D W n ∗ W p + W n ∗ W d B V 2 = 1 2 W d ∗ E m a x 2 = 1 2 q ( N A W p − N D W n ∗ ) W d ϵ ( W p + W n ∗ ) ( W d + N A W p − N D W n ∗ N D W d W p + W n ∗ ) B V 2 = 2 1 W d ∗ E ma x 2 = 2 1 ϵ ( W p + W n ∗ ) q ( N A W p − N D W n ∗ ) W d ( W d + N D N A W p − N D W n ∗ W p + W n ∗ W d )
终端区击穿电压为2部分计算结果之和
B V i m b a l a n c e = B V 1 + B V 2 = 1 2 W d q N D W n ∗ ϵ + 1 2 q ( N A W p − N D W n ∗ ) W d ϵ ( W p + W n ∗ ) ( W d + N A W p − N D W n ∗ N D W d W p + W n ∗ ) B V imba l an ce = B V 1 + B V 2 = 2 1 W d ϵ q N D W n ∗ + 2 1 ϵ ( W p + W n ∗ ) q ( N A W p − N D W n ∗ ) W d ( W d + N D N A W p − N D W n ∗ W p + W n ∗ W d ) B V i m b a l a n c e = 1 2 W d q N A W p ϵ + 1 2 W d q ( N A W p − N D W n ∗ ) ϵ ( W d W p + W n ∗ − 1 + W d ( N A W p − N D W n ∗ ) N D ( W p + W n ∗ ) 2 ) B V imba l an ce = 2 1 W d ϵ q N A W p + 2 1 W d ϵ q ( N A W p − N D W n ∗ ) ( W p + W n ∗ W d − 1 + N D ( W p + W n ∗ ) 2 W d ( N A W p − N D W n ∗ ) ) B V b a l a n c e B V ba l an ce W d W p + W n ∗ > > 1 W p + W n ∗ W d >> 1 N A W p > N D W n ∗ N A W p > N D W n ∗ B V i m b a l a n c e > B V b a l a n c e B V imba l an ce > B V ba l an ce
三、仿真设置及结果
物理模型设置
3.1 连续性方程
∇ ⋅ J n − ∑ j R n t j − R s p − R s t − R a u + G o p t ( t ) = ∂ n ∂ t + N D ∂ f D ∂ t ∇ ⋅ J n − j ∑ R n t j − R s p − R s t − R a u + G o pt ( t ) = ∂ t ∂ n + N D ∂ t ∂ f D ∇ ⋅ J p + ∑ j R p t j + R s p + R s t + R a u − G o p t ( t ) = − ∂ p ∂ t + N A ∂ f A ∂ t ∇ ⋅ J p + j ∑ R p t j + R s p + R s t + R a u − G o pt ( t ) = − ∂ t ∂ p + N A ∂ t ∂ f A 3.2 泊松方程
− ∇ ⋅ ( ϵ 0 ϵ d c q ∇ V ) = − n + p + N D ( 1 − f D ) − N A f A + ∑ j N t j ( δ j − f t j ) − ∇ ⋅ ( q ϵ 0 ϵ d c ∇ V ) = − n + p + N D ( 1 − f D ) − N A f A + j ∑ N t j ( δ j − f t j ) 3.3 低场和高场迁移率模型
低场迁移率模型(Masetti Model)
μ 0 = μ min 1 e − P c N i + μ max ( T L T 0 ) − ζ − μ min 2 1 + ( N i C r ) α − μ 1 1 + ( C s N i ) β μ 0 = μ m i n 1 e − N i P c + 1 + ( C r N i ) α μ m a x ( T 0 T L ) − ζ − μ m i n 2 − 1 + ( N i C s ) β μ 1
高场迁移率模型(Canali Model)
μ n = μ 0 n ( 1 + ( μ 0 n F / v s n ) β n ) 1 / β n μ n = ( 1 + ( μ 0 n F / v s n ) β n ) 1/ β n μ 0 n μ p = μ 0 p ( 1 + ( μ 0 p F / v s p ) β p ) 1 / β p μ p = ( 1 + ( μ 0 p F / v s p ) β p ) 1/ β p μ 0 p
3.4 体缺陷模型
Shockley-Read-Hall Model
R n t j = c n j n N t j ( 1 − f t j ) − c n j n 1 j N t j f t j R n t j = c nj n N t j ( 1 − f t j ) − c nj n 1 j N t j f t j R p t j = c p j p N t j f t j − c p j p 1 j N t j ( 1 − f t j ) R p t j = c p j p N t j f t j − c p j p 1 j N t j ( 1 − f t j ) N t j ∂ f t j ∂ t = R n t j − R p t j N t j ∂ t ∂ f t j = R n t j − R p t j
c n j = σ n j v n = σ n j 8 k T π m n c nj = σ nj v n = σ nj π m n 8 k T c p j = σ p j v p = σ p j 8 k T π m p c p j = σ p j v p = σ p j π m p 8 k T 1 τ n j = c n j N t j ; 1 τ n j = c n j N t j τ nj 1 = c nj N t j ; τ nj 1 = c nj N t j 3.5 碰撞电离模型
Okuto Model
α ( F ava ) = a ⋅ ( 1 + c ( T − T 0 ) ) F ava γ exp [ − ( b [ 1 + d ( T − T 0 ) ] F ava ) δ ] α ( F ava ) = a ⋅ ( 1 + c ( T − T 0 ) ) F ava γ exp [ − ( F ava b [ 1 + d ( T − T 0 ) ] ) δ ]
仿真参数设置
在此项工作中,P柱宽度设置为W p = 5 μ W p = 5 μ N A = 3 × 1 0 15 c m − 3 N A = 3 × 1 0 15 c m − 3 W n = 12 μ W n = 12 μ W n ∗ = 10 μ W n ∗ = 10 μ N D = 9 × 1 0 14 c m − 3 N D = 9 × 1 0 14 c m − 3 1 × 1 0 17 c m − 3 1 × 1 0 17 c m − 3 1 × 1 0 20 c m − 3 1 × 1 0 20 c m − 3 5 × 1 0 16 c m − 3 5 × 1 0 16 c m − 3
仿真结果
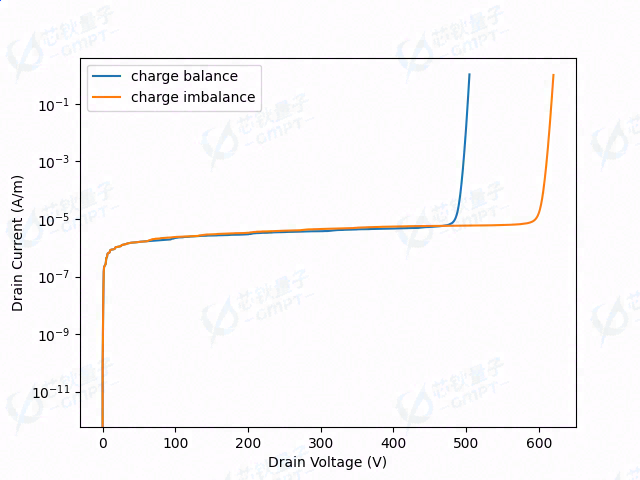
图8. 2种终端结构的击穿曲线
如图8所示,2种终端结构在击穿前的漏电流基本相等,约为5 × 1 0 − 6 A / m 5 × 1 0 − 6 A / m
四、总结
本文首先简述了超结VDMOS器件的基本原理,然后研究了电荷平衡与电荷不平衡2种终端结构,由理论推导得出了电荷不平衡终端击穿电压大于电荷平衡终端击穿电压的结论,最后使用Nuwa TCAD软件仿真2种终端结构的击穿电压从而验证了该结论的正确性。
参考文献
[1] Q. Qian, W. Sun, J. Zhu and S. Liu, A Novel Charge-Imbalance Termination for Trench Superjunction VDMOS, IEEE Electron Device Lett., vol. 31, no. 12, Dec. 2010.
[2] H. Wang, E. Napoli, and F. Udrea, Breakdown voltage for superjunction power devices with charge imbalance: An analytical model valid for both punch through and non punch through devices, IEEE Trans Electron Devices, vol. 56, no. 12, Dec. 2009.
[3] E. Napoli, H. Wang, and F. Udrea, The effect of charge imbalance on superjunction power devices: An exact analytical solution, IEEE Electron Device Lett., vol. 29, no. 3, Mar. 2008.