使用Nuwa TCAD软件仿真超结VDMOS器件
GMPT, 2024/05/27
摘要: 垂直双扩散金属氧化物半导体场效应晶体管(Vertical Double-Diffused Metal Oxide Semiconductor Field Effect Transistor, VDMOS),是一种单极型功率开关器件,具有开关速度快、静态输入阻抗高的优点,被广泛应用于电机调速、雷达、开关电源、汽车电子、逆变器、移动通信等领域。超结VDMOS在传统 VDMOS结构的基础上引入了超结结构,代替了原漂移区的轻掺杂结构,使得器件处于反偏状态时,在横向电场的作用下N型半导体与P型半导体的电荷相互补偿耗尽,超结区域形成横向耐压层,从而提升器件的反向击穿电压。
本文将基于Nuwa TCAD软件对超结VDMOS器件进行仿真,并展示软件仿真结果。
一、器件结构
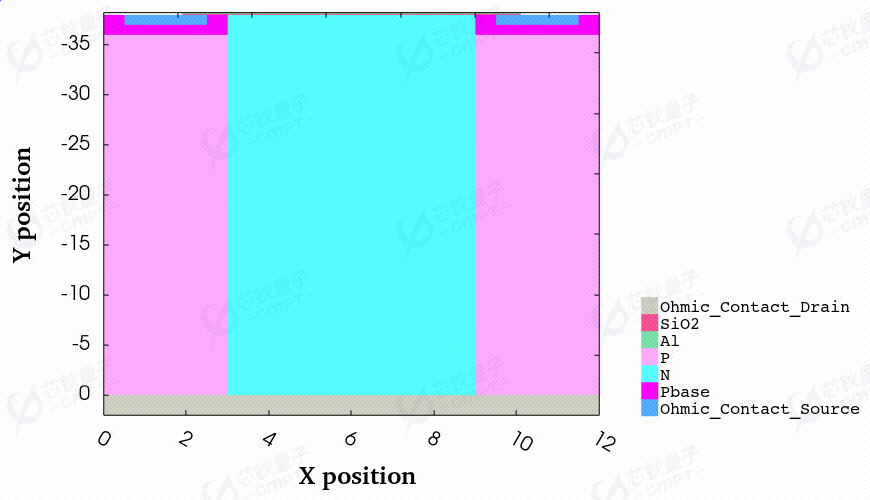
图1. 超结VDMOS器件结构示意图
在此项工作中,超结VDMOS器件结构如图1所示。其中,P柱高度设置为36μ μ μ μ 2 × 1 0 15 c m − 3 2 × 1 0 15 c m − 3 5 × 1 0 16 c m − 3 5 × 1 0 16 c m − 3 5 × 1 0 19 c m − 3 5 × 1 0 19 c m − 3 1 × 1 0 18 c m − 3 1 × 1 0 18 c m − 3 μ μ
二、物理模型设置
2.1 连续性方程
∇ ⋅ J n − ∑ j R n t j − R s p − R s t − R a u + G o p t ( t ) = ∂ n ∂ t + N D ∂ f D ∂ t ∇ ⋅ J n − j ∑ R n t j − R s p − R s t − R a u + G o pt ( t ) = ∂ t ∂ n + N D ∂ t ∂ f D ∇ ⋅ J p + ∑ j R p t j + R s p + R s t + R a u − G o p t ( t ) = − ∂ p ∂ t + N A ∂ f A ∂ t ∇ ⋅ J p + j ∑ R p t j + R s p + R s t + R a u − G o pt ( t ) = − ∂ t ∂ p + N A ∂ t ∂ f A 2.2 泊松方程
− ∇ ⋅ ( ϵ 0 ϵ d c q ∇ V ) = − n + p + N D ( 1 − f D ) − N A f A + ∑ j N t j ( δ j − f t j ) − ∇ ⋅ ( q ϵ 0 ϵ d c ∇ V ) = − n + p + N D ( 1 − f D ) − N A f A + j ∑ N t j ( δ j − f t j ) 2.3 低场和高场迁移率模型
低场迁移率模型(Masetti Model)
μ 0 = μ min 1 e − P c N i + μ max ( T L T 0 ) − ζ − μ min 2 1 + ( N i C r ) α − μ 1 1 + ( C s N i ) β μ 0 = μ m i n 1 e − N i P c + 1 + ( C r N i ) α μ m a x ( T 0 T L ) − ζ − μ m i n 2 − 1 + ( N i C s ) β μ 1
高场迁移率模型(Canali Model)
μ n = μ 0 n ( 1 + ( μ 0 n F / v s n ) β n ) 1 / β n μ n = ( 1 + ( μ 0 n F / v s n ) β n ) 1/ β n μ 0 n μ p = μ 0 p ( 1 + ( μ 0 p F / v s p ) β p ) 1 / β p μ p = ( 1 + ( μ 0 p F / v s p ) β p ) 1/ β p μ 0 p
2.4 界面缺陷模型
Exponential tail Model
DOS ( E ) = N t r a p E t a i l e [ − ( E − E 0 ) E t a i l ] DOS ( E ) = E t ai l N t r a p e [ − E t ai l ( E − E 0 ) ]
Gaussian Model
DOS ( E ) = N t r a p 2 π σ e [ − ( E − E 0 ) 2 2 σ 2 ] DOS ( E ) = 2 π σ N t r a p e [ − 2 σ 2 ( E − E 0 ) 2 ]
2.5 体缺陷模型
Shockley-Read-Hall Model
R n t j = c n j n N t j ( 1 − f t j ) − c n j n 1 j N t j f t j R n t j = c nj n N t j ( 1 − f t j ) − c nj n 1 j N t j f t j R p t j = c p j p N t j f t j − c p j p 1 j N t j ( 1 − f t j ) R p t j = c p j p N t j f t j − c p j p 1 j N t j ( 1 − f t j ) N t j ∂ f t j ∂ t = R n t j − R p t j N t j ∂ t ∂ f t j = R n t j − R p t j c n j = σ n j v n = σ n j 8 k T π m n c nj = σ nj v n = σ nj π m n 8 k T c p j = σ p j v p = σ p j 8 k T π m p c p j = σ p j v p = σ p j π m p 8 k T 1 τ n j = c n j N t j ; 1 τ n j = c n j N t j τ nj 1 = c nj N t j ; τ nj 1 = c nj N t j
Gaussian Model
DOS ( E ) = N t r a p 2 π σ e [ − ( E − E 0 ) 2 2 σ 2 ] DOS ( E ) = 2 π σ N t r a p e [ − 2 σ 2 ( E − E 0 ) 2 ]
2.6 碰撞电离模型
Okuto Model
α ( F ava ) = a ⋅ ( 1 + c ( T − T 0 ) ) F ava γ exp [ − ( b [ 1 + d ( T − T 0 ) ] F ava ) δ ] α ( F ava ) = a ⋅ ( 1 + c ( T − T 0 ) ) F ava γ exp [ − ( F ava b [ 1 + d ( T − T 0 ) ] ) δ ]
三、结果与讨论
3.1 反向加压电势分布
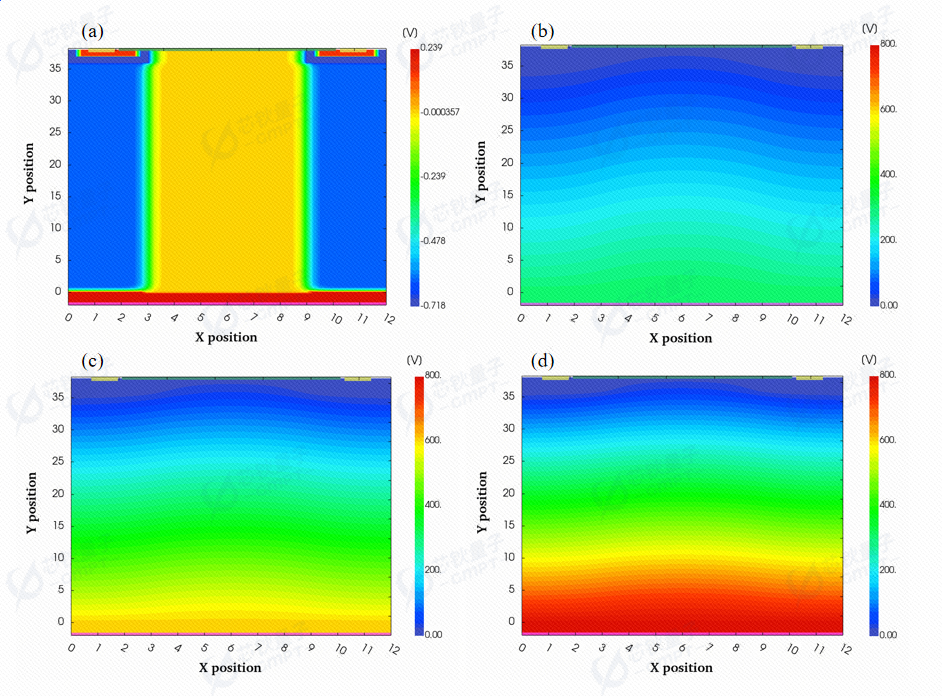
图2. 超结VDMOS器件在 (a)平衡态 (b)反向加压300V (c)反向加压600V (d)反向击穿 时的电势分布
上图展示了超结VDMOS器件从平衡态开始加反向电压直到反向击穿的电势分布情况。
3.2 反向击穿特性
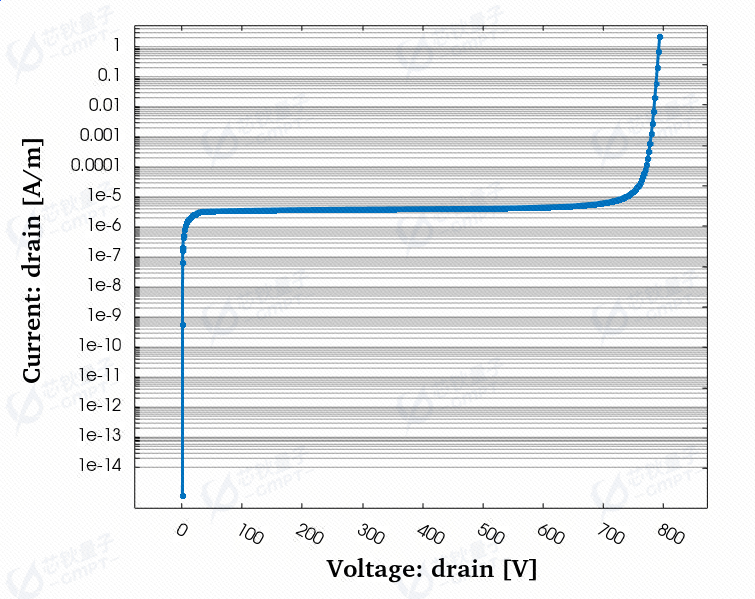
图3. 超结VDMOS器件的反向击穿曲线
如图可知,反向击穿之前漏电流约为$5\times 10^{-6}A/m$,在击穿电压附近漏电流急剧增大,发生雪崩击穿,反向击穿电压约为790V。
3.3 阈值电压
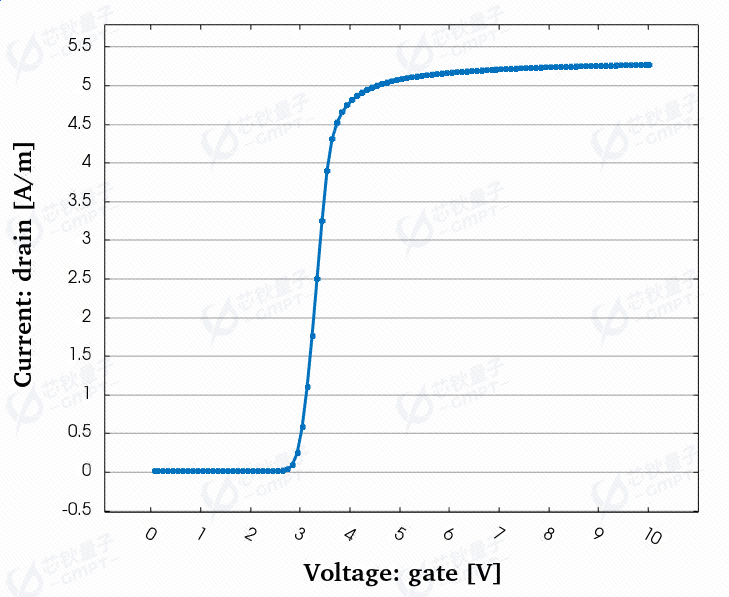
图4. 超结VDMOS器件的阈值电压
如图可知,超结VDMOS器件的阈值电压约为2.8V。
3.4 转移特性
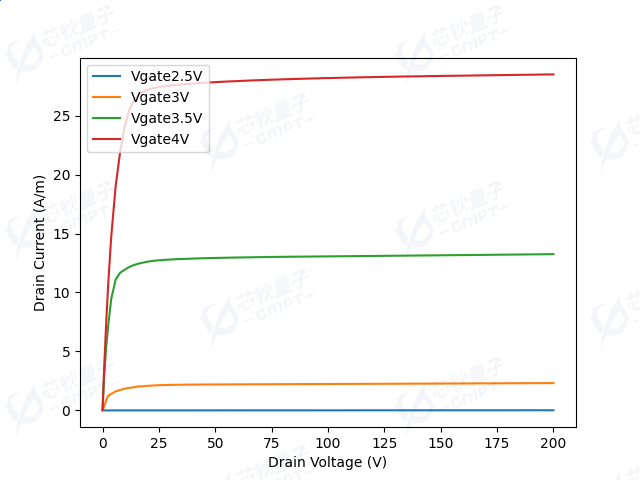
图5. 超结VDMOS器件在不同栅压下的转移特性
图5展示了超结VDMOS器件在栅压分别为2.5V,3V, 3.5V和4V下的转移特性。已知器件的阈值电压为2.8V,所以栅压为2.5V时器件沟道未打开,器件此时没有正向输出。当栅压大于阈值电压后,器件沟道打开并开始正向输出,随着栅压增大器件的输出也随之增强,漏电流也在漏极电压增大之后趋于饱和。
四、总结
本文对超结VDMOS器件进行了仿真,介绍了仿真中引用的物理模型,并展示了器件的仿真结果,包括反向加压电势分布、反向击穿特性、阈值电压和不同栅压下的转移特性。
参考文献
[1] 李吕强,超结器件工艺窗口改善与可靠性提升,电子科技大学硕士学位论文