使用Nuwa TCAD软件仿真PGaN_E-HEMT_FP器件

GMPT, 2025/3/3

注：本文和相关案例为上海芯钬量子科技有限公司与甬江实验室精准光子集成研究中心施跃春教授团队联合开发。

一、器件结构

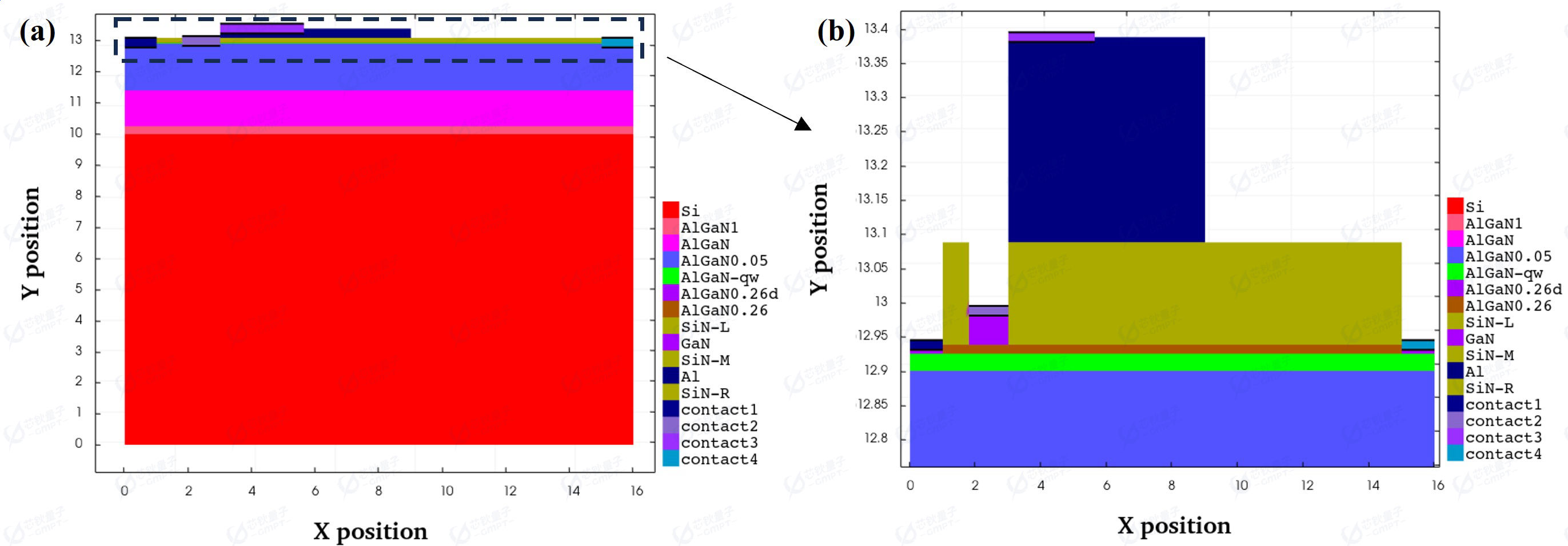
图1 PGaN_E-HEMT_FP 器件结构

在本项工作中，硅(Si)衬底的P-GaN增强型栅场板HEMT器件结构如图1所示。硅(Si)衬底的厚度为10μm，宽度为16μm；AlGaN成核层(nucleation layer)厚度为0.25μm，其中Al组分为1；缓冲层(buffer layer)由厚度为1.15μm，Al组分为0以及厚度为1.5μm，Al组分为0.05的AlGaN组成；AlGaN沟道层(channel layer)厚度为25nm，其中Al组分为0；AlGaN势垒层(barrier layer)厚度为13nm，其中Al组分为0.26；帽层 (spacer) 厚度为0.15μm，宽度为12.8μm；帽层左侧被P掺杂的厚度为50nm的GAN隔开。金属Al厚度为0.3μm，宽度为6μm。漏极和源极为欧姆接触位于器件左右两端宽度为1μm，栅极为肖特基接触位于GaN上方宽度为1.2μm。常规p-GaN增强型HEMT器件为三端结构，具有欧姆接触的源、漏端和肖特基接触的栅端。本结构在Al上方引入一个额外的场板电极端。

二、物理模型设置

2.1 有源区载流子输运模型

$$\begin{array}{c}{\displaystyle R_{qw}=\frac{n-n_0}{\tau };\frac{1}{\tau }=\frac{1}{{\tau }_{300}}{e}^{(-\frac{T-300}{{\tau }_0})}}\\ {\displaystyle \frac{d{n}_t}{dt}=-\frac{n_t}{{\tau }_{\text{interb }}}+J_{\text{in }}+J_{out}-J_{fesc}}\\ {\displaystyle J_{fesc}=\frac{F_{\text{esc }}{n}_t{V}_{\text{fesc }}}{d};{\tau }_{\text{fesc }}=\frac{d}{V_{fesc}{F}_{\text{esc }}}}\end{array}\backslash begin\{gathered\}\; R\_\{q\; w\}=\backslash frac\{n-n\_0\}\{\backslash tau\}\; ;\; \backslash frac\{1\}\{\backslash tau\}=\backslash frac\{1\}\{\backslash tau\_\{300\}\}\; e^\{\backslash left(-\backslash frac\{T-300\}\{\backslash tau\_0\}\backslash right)\}\; \backslash \backslash \; \backslash frac\{d\; n\_t\}\{d\; t\}=-\backslash frac\{n\_t\}\{\backslash tau\_\{\backslash text\; \{interb\; \}\}\}+J\_\{\backslash text\; \{in\; \}\}+J\_\{o\; u\; t\}-J\_\{f\; e\; s\; c\}\; \backslash \backslash \; J\_\{f\; e\; s\; c\}=\backslash frac\{F\_\{\backslash text\; \{esc\; \}\}\; n\_t\; V\_\{\backslash text\; \{fesc\; \}\}\}\{d\}\; ;\; \backslash quad\; \backslash tau\_\{\backslash text\; \{fesc\; \}\}=\backslash frac\{d\}\{V\_\{f\; e\; s\; c\}\; F\_\{\backslash text\; \{esc\; \}\}\}\; \backslash end\{gathered\}$$

2.2 连续性方程

2.3 泊松方程 $$\begin{array}{c}{\displaystyle -\mathrm{\nabla }\cdot \left(\frac{{ϵ}_0{ϵ}_{dc}}{q}\mathrm{\nabla }V\right)=-n+p+N_D(1-f_D)-N_A{f}_A+\sum _j{N}_{tj}({\delta }_j-f_{tj})}\end{array}\backslash begin\{aligned\}\; -\backslash nabla\; \backslash cdot\backslash left(\backslash frac\{\backslash epsilon\_0\; \backslash epsilon\_\{d\; c\}\}\{q\}\; \backslash nabla\; V\backslash right)=-n+p+N\_D\backslash left(1-f\_D\backslash right)-N\_A\; f\_A+\backslash sum\_j\; N\_\{t\; j\}\backslash left(\backslash delta\_j-f\_\{t\; j\}\backslash right)\; \backslash end\{aligned\}$$

2.4 低场和高场迁移率模型

  低场迁移率模型 (Masetti Model)

$$\begin{array}{c}{\displaystyle {\mu }_0={\mu }_{\min 1}{e}^{-\frac{P_c}{N_i}}+\frac{{\mu }_{\max }{\left(\frac{T_L}{T_0}\right)}^{-\zeta }-{\mu }_{\min 2}}{1+{\left(\frac{N_i}{C_r}\right)}^{\alpha }}-\frac{{\mu }_1}{1+{\left(\frac{C_s}{N_i}\right)}^{\beta }}}\end{array}\backslash begin\{aligned\}\; \backslash mu\_0=\backslash mu\_\{\backslash min\; 1\}\; e^\{-\backslash frac\{P\_c\}\{N\_i\}\}+\backslash frac\{\backslash mu\_\{\backslash max\; \}\backslash left(\backslash frac\{T\_L\}\{T\_0\}\backslash right)^\{-\backslash zeta\}-\backslash mu\_\{\backslash min\; 2\}\}\{1+\backslash left(\backslash frac\{N\_i\}\{C\_r\}\backslash right)^\backslash alpha\}-\backslash frac\{\backslash mu\_1\}\{1+\backslash left(\backslash frac\{C\_s\}\{N\_i\}\backslash right)^\backslash beta\}\; \backslash end\{aligned\}$$

  高场迁移率模型 (Canali Model)

$$\begin{array}{c}{\displaystyle {\mu }_n=\frac{{\mu }_{0n}}{{(1+{\left({\mu }_{0n}F\mathrm{/}{v}_{sn}\right)}^{{\beta }_n})}^{1\mathrm{/}{\beta }_n}}}\\ {\displaystyle {\mu }_p=\frac{{\mu }_{0p}}{{(1+{\left({\mu }_{0p}F\mathrm{/}{v}_{sp}\right)}^{{\beta }_p})}^{1\mathrm{/}{\beta }_p}}}\end{array}\backslash begin\{aligned\}\; \backslash mu\_n=\backslash frac\{\backslash mu\_\{0\; n\}\}\{\backslash left(1+\backslash left(\backslash mu\_\{0\; n\}\; F\; /\; v\_\{s\; n\}\backslash right)^\{\backslash beta\_n\}\backslash right)^\{1\; /\; \backslash beta\_n\}\}\; \backslash \backslash \; \backslash mu\_p=\backslash frac\{\backslash mu\_\{0\; p\}\}\{\backslash left(1+\backslash left(\backslash mu\_\{0\; p\}\; F\; /\; v\_\{s\; p\}\backslash right)^\{\backslash beta\_p\}\backslash right)^\{1\; /\; \backslash beta\_p\}\}\; \backslash end\{aligned\}$$

2.5 陷阱模型 (Trap Model)

2.6 极化模型 (Polarization Model)

2.7 热电子发射模型

三、工作原理及结果讨论

3.1 能带分布

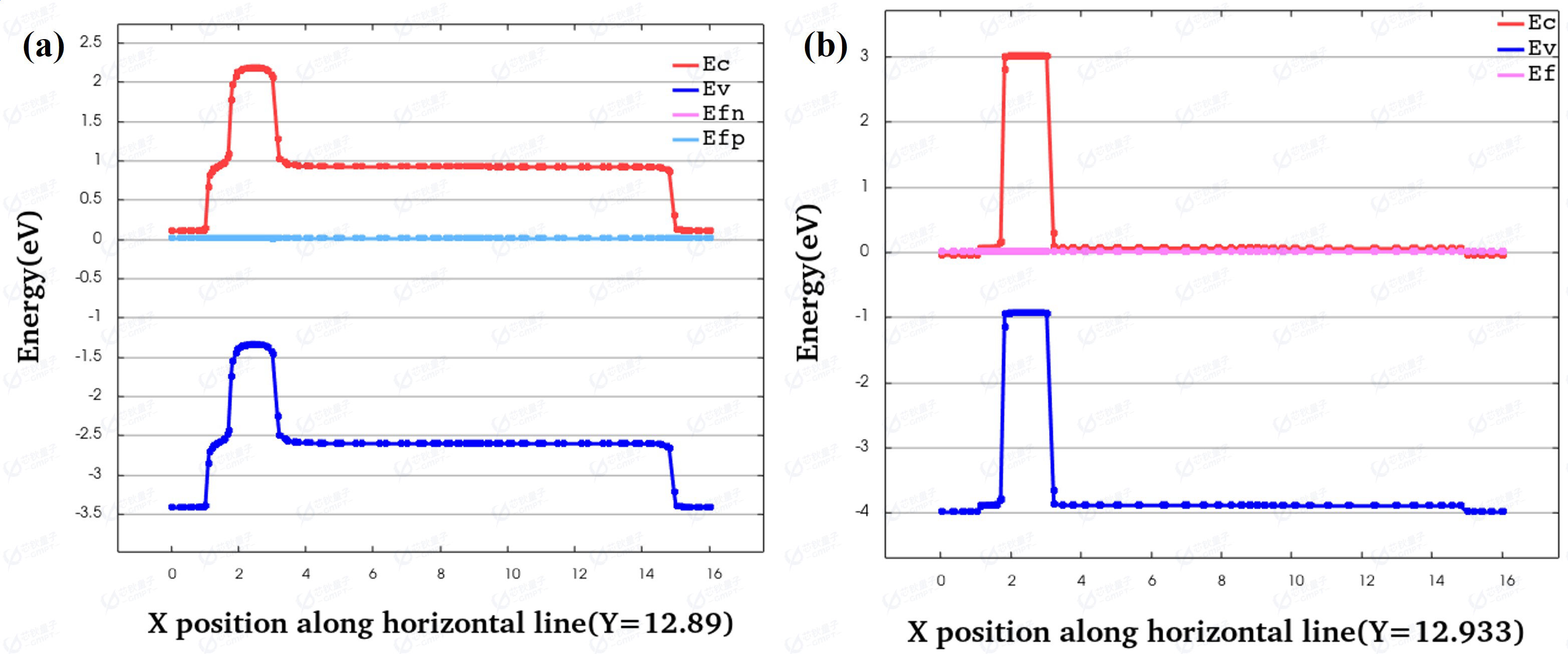
图2 (a)Al_0.05GaN和GaN界面能带分布 (b)Al_0.26GaN和GaN界面能带分布

Y=12.89位于Al_0.05GaN和GaN的接触面附近，Y=12.933位于Al_0.26GaN和GaN的接触面附近。AlGaN/GaN 异质结界面由极化产生的电荷密度由自发极化和压电极化共同决定，极化效应的差异使得空穴在异质结界面产生，而空穴可以通过电荷感应在下方产生大量电子，导电沟道2DGE由此产生。由于Al_0.05GaN超过了临界厚度且Al组分小于Al_0.26GaN，因此在异质结界面产生的2DGE浓度远小于Al_0.26GaN/GaN。相应的图2(b)中的导带相比于图2(a)更加靠近费米能级。由于Al_0.26GaN两端存在n掺杂，因此能带两端导带下移。而在栅极P-GaN下方，2DGE被耗尽，导带上移远离费米能级。

3.2 平衡态

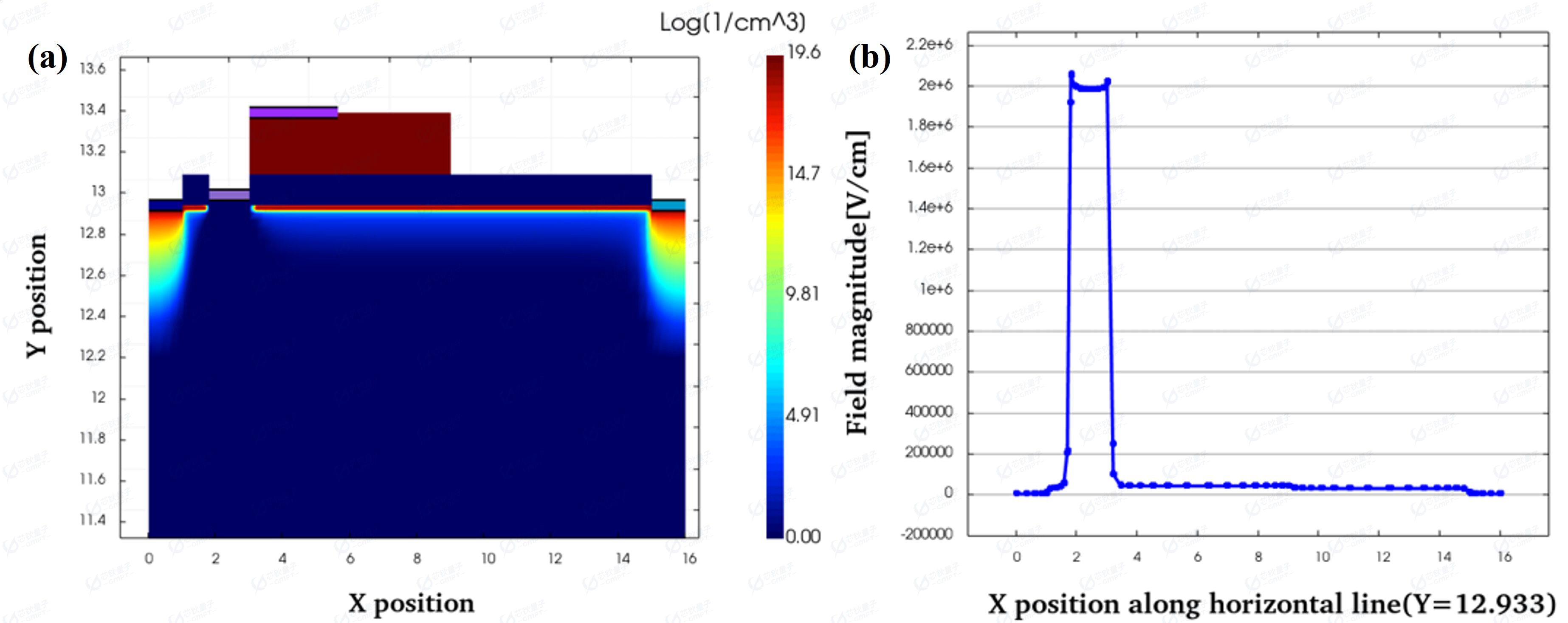
图3 (a)平衡态2DGE（b）平衡态器件场强

P-GaN 栅增强型 HEMT 器件是在常规 HEMT 器件的栅金属电极与势垒层之间插入一层 P 型掺杂的 GaN，形成自上而下的电场，下方2DEG中的电子被“拉走”或“耗尽”如图3(a)，使器件在无栅压偏置条件下处于关断状态。受AlGaN/GaN内建电场及P-GaN外加电场的影响，栅极下方电场强度很大如图3(b)所示。

3.3 无场板电场强度

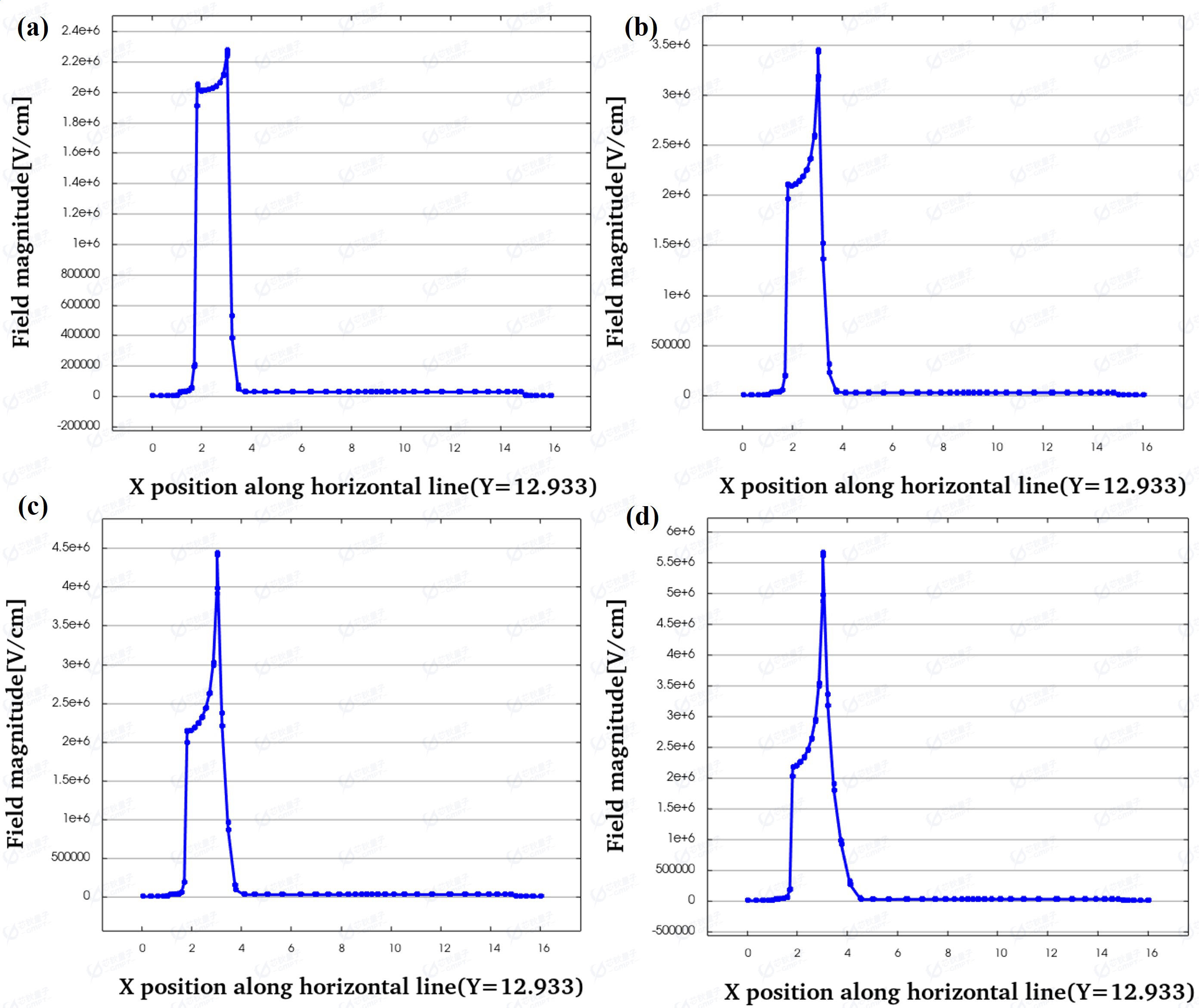
图4 电场强度

当GaN HEMT工作在关态高漏极偏置状态时，会产生自栅电极漏侧边缘向漏电极方向逐渐扩展的耗尽区，该区域中的电子被耗尽留下带正电的固定电荷。耗尽区的正电中心会产生由正电中心出发指向低电位栅电极的电力线，在栅电极漏侧边缘产生电力线集聚效应，形成电场峰值[1]。当栅电极漏侧边缘电场强度超过 GaN 材料自身的击穿电场强度时，在该处热电子碰撞会产生电子与空穴对，电子与空穴继续碰撞电离，最终导致器件发生雪崩击穿。图4(a), (b), (c), (d)分别为未加场板时漏极电压为10V, 50V, 100V, 200V对应的电场强度。可以看出栅电极下方沟道耗尽区承担源漏间高电压，在栅电极漏侧边缘电场强度远远高于栅极下方区域。

3.4 添加场板后电场强度

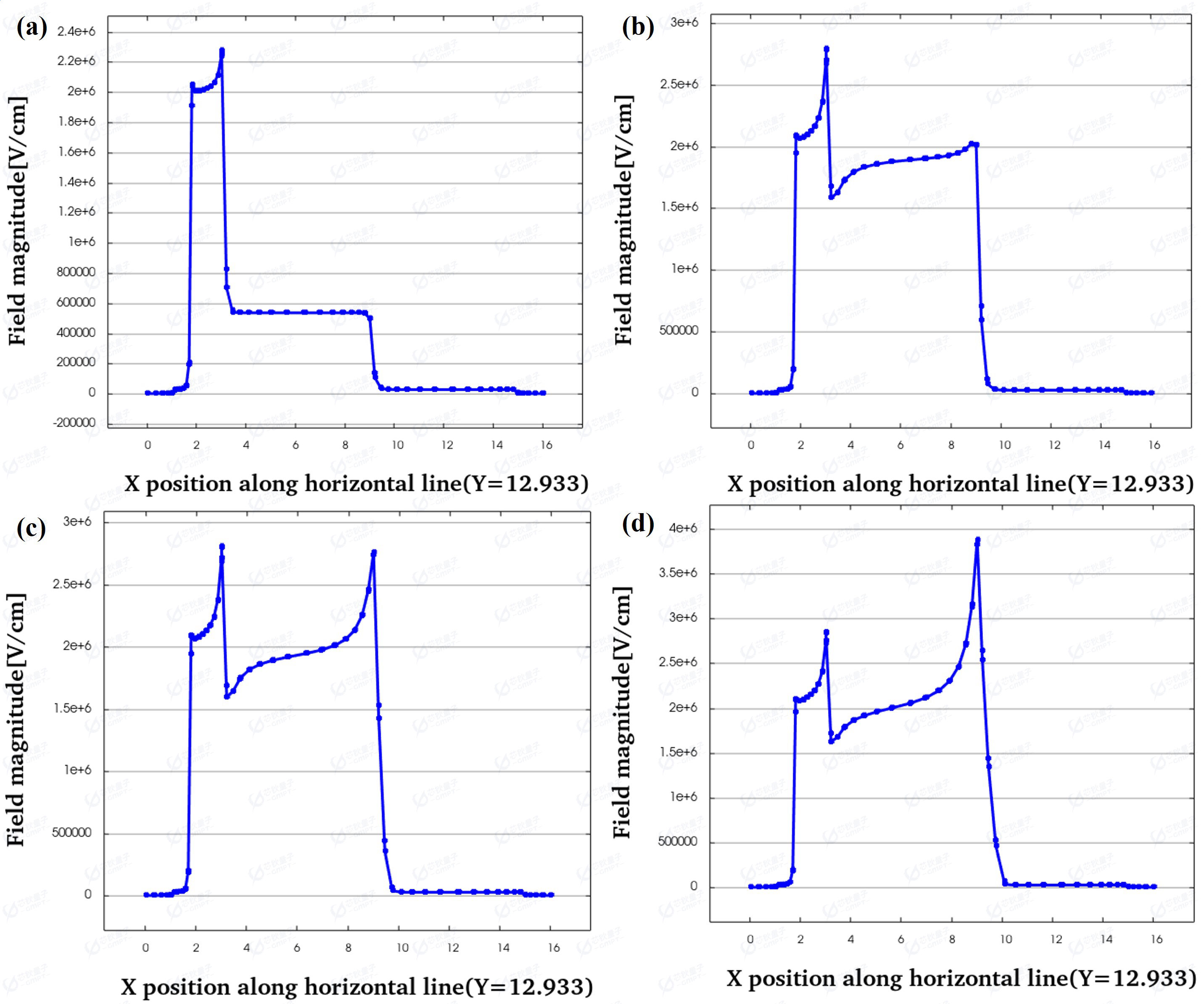
图5 电场强度

引入场板结构可以理解为在钝化层表面引入负的等效电荷，形成由正电中心出发，终止于表面负电荷的电力线，形成纵向电场，拓展了耗尽区。等效负电荷还会在器件内部引入与栅电极漏侧边缘原有电场方向相反的横向电场，以降低栅电极处原有的电场峰值，从而提高了器件的击穿电压；同时在靠近漏极的场板边缘处，等效负电荷产生的电场相互叠加产生新的电场峰值。图5(a), (b), (c), (d)分别为添加场板后漏极电压为10V, 50V, 100V, 200V对应的电场强度。可以看出加入场板后栅电极漏侧边缘的电场峰值大大减小，从而增大了器件的击穿电压。

四、总结

本文对PGaN_E-HEMT_FP器件进行仿真，介绍了仿真中引用的物理模型的公式，并展示了器件的仿真结果，包括能带结构和场板机理。通过Nuwa TCAD软件得到的仿真结果，本文进一步分析了器件内部机理，包括能带分布、载流子迁移、二维电子气、击穿电压等，为PGaN_E-HEMT_FP器件结构分析和器件性能提升提供了思路。

参考文献

[1] 霍腾，GaN基HEMT器件新型场板结构设计与工艺研究，电子科技大学硕士论文