使用Nuwa TCAD软件仿真和设计增强型p-GaN HEMT器件

GMPT, 2024/07/09

  第三代半导体材料GaN具有宽禁带、高电子饱和速度和良好导热性等优点，其中GaN高电子迁移率晶体管（HEMT）具有高电场强度、高迁移率、良好热稳定性，在高频、大功率应用环境下具有突出优势。但大多数AlGaN/GaN HEMT都是常开型，在实际大功率开关应用中不够安全。因此，市场迫切需要AlGaN/GaN HEMT在保持低导通电阻的同时，实现常断工作。为了满足这些要求，本文引入p型GaN插入层结构，利用从p型栅端到二维电子气（2DEG）的空穴注入实现电导调制，有效地降低栅下沟道中的2DEG密度。本文将基于Nuwa TCAD软件对p-GaN HEMT进行相关仿真和设计，并展示软件仿真结果。

一、器件结构

图1. AlGaN/GaN p-GaN HEMT器件结构

  在本项工作中，硅（Si）异质衬底的AlGaN/GaN HEMT器件结构如图1所示。其中，p-GaN栅极厚度为50nm, 掺杂浓度为$5\times 10^{19}{cm}^{-3}5\backslash times\; 10^\{19\}\; \{cm\}^\{-3\}$；AlGaN势垒层（barrier layer）厚度为13nm，其中Al组分为0.26；GaN沟道层（channel layer）厚度为25nm；AlGaN反势垒层（back barrier layer）厚度为60nm，其中Al组分为0.05；GaN缓冲层（buffer layer）厚度为3$\mu \backslash mu$m；AlN成核层（nucleation layer）厚度为0.2$\mu \backslash mu$m；另外，漏极、栅极和源极均为欧姆接触，宽度都为1$\mu \backslash mu$m。其中，栅-源间距（L_GS）和漏-栅（L_GD) 间距分别为0.8$\mu \backslash mu$m和12$\mu \backslash mu$m。

二、物理模型设置

2.1 热电子发射模型

2.2 连续性方程

$$\begin{array}{c}{\displaystyle \mathrm{\nabla }\cdot J_n-\sum _j{R}_n^{tj}-R_{sp}-R_{st}-R_{au}+G_{opt}(t)=\frac{\mathrm{\partial }n}{\mathrm{\partial }t}+N_D\frac{\mathrm{\partial }{f}_D}{\mathrm{\partial }t}}\end{array}\backslash begin\{aligned\}\; \backslash nabla\; \backslash cdot\; J\_n-\backslash sum\_j\; R\_n^\{t\; j\}-R\_\{s\; p\}-R\_\{s\; t\}-R\_\{a\; u\}+G\_\{o\; p\; t\}(t)=\backslash frac\{\backslash partial\; n\}\{\backslash partial\; t\}+N\_D\; \backslash frac\{\backslash partial\; f\_D\}\{\backslash partial\; t\}\; \backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle \mathrm{\nabla }\cdot J_p+\sum _j{R}_p^{tj}+R_{sp}+R_{st}+R_{au}-G_{opt}(t)=-\frac{\mathrm{\partial }p}{\mathrm{\partial }t}+N_A\frac{\mathrm{\partial }{f}_A}{\mathrm{\partial }t}}\end{array}\backslash begin\{aligned\}\; \backslash nabla\; \backslash cdot\; J\_p+\backslash sum\_j\; R\_p^\{t\; j\}+R\_\{s\; p\}+R\_\{s\; t\}+R\_\{a\; u\}-G\_\{o\; p\; t\}(t)=-\backslash frac\{\backslash partial\; p\}\{\backslash partial\; t\}+N\_A\; \backslash frac\{\backslash partial\; f\_A\}\{\backslash partial\; t\}\; \backslash end\{aligned\}$$

2.3 泊松方程

$$-\mathrm{\nabla }\cdot \left(\frac{{ϵ}_0{ϵ}_{dc}}{q}\mathrm{\nabla }V\right)=-n+p+N_D(1-f_D)-N_A{f}_A+\sum _j{N}_{tj}({\delta }_j-f_{tj})-\backslash nabla\; \backslash cdot\backslash left(\backslash frac\{\backslash epsilon\_0\; \backslash epsilon\_\{d\; c\}\}\{q\}\; \backslash nabla\; V\backslash right)=-n+p+N\_D\backslash left(1-f\_D\backslash right)-N\_A\; f\_A+\backslash sum\_j\; N\_\{t\; j\}\backslash left(\backslash delta\_j-f\_\{t\; j\}\backslash right)$$

2.4 低场和高场迁移率模型

低场迁移率模型

高场迁移率模型 (Canali Model)

2.5 漏极和源极重掺杂实现欧姆接触 Tunneling Model

2.6 界面缺陷模型 Exponential tail Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{E_{tail}}{e}^{[-\frac{(E-E_0)}{E_{tail}}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{E\_\{\; \{tail\; \}\}\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)\}\{E\_\{\{tail\; \}\}\}\backslash right]\}$$

Gaussian Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.7 体缺陷模型 Shockley-Read-Hall Model

$$\begin{array}{c}{\displaystyle R_n^{tj}=c_{nj}n{N}_{tj}(1-f_{tj})-c_{nj}{n}_{1j}{N}_{tj}{f}_{tj}}\end{array}\backslash begin\{aligned\}R\_n^\{t\; j\}=c\_\{n\; j\}\; n\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)-c\_\{n\; j\}\; n\_\{1\; j\}\; N\_\{t\; j\}\; f\_\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle R_p^{tj}=c_{pj}p{N}_{tj}{f}_{tj}-c_{pj}{p}_{1j}{N}_{tj}(1-f_{tj})}\end{array}\backslash begin\{aligned\}R\_p^\{t\; j\}=c\_\{p\; j\}\; p\; N\_\{t\; j\}\; f\_\{t\; j\}-c\_\{p\; j\}\; p\_\{1\; j\}\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle N_{tj}\frac{\mathrm{\partial }{f}_{tj}}{\mathrm{\partial }t}=R_n^{tj}-R_p^{tj}}\end{array}\backslash begin\{aligned\}N\_\{t\; j\}\; \backslash frac\{\backslash partial\; f\_\{t\; j\}\}\{\backslash partial\; t\}=R\_n^\{t\; j\}-R\_p^\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle c_{nj}={\sigma }_{nj}{v}_n={\sigma }_{nj}\sqrt{\frac{8kT}{\pi m_n}};c_{pj}={\sigma }_{pj}{v}_p={\sigma }_{pj}\sqrt{\frac{8kT}{\pi m_p}}}\end{array}\backslash begin\{aligned\}c\_\{n\; j\}=\backslash sigma\_\{n\; j\}\; v\_n=\backslash sigma\_\{n\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_n\}\}\; ;\; \backslash quad\; c\_\{p\; j\}=\backslash sigma\_\{p\; j\}\; v\_p=\backslash sigma\_\{p\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_p\}\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle \frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj};\frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj}}\end{array}\backslash begin\{aligned\}\backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\};\; \backslash quad\; \backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\}\backslash end\{aligned\}$$

Gaussian Model $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.8 极化模型

$$P_{sp}=-0.090x-0.034(1-x)+0.019x(1-x)\text{ for }A{l}_{x}G{a}_{1-x}NP\_\{s\; p\}=-0.090\; x-0.034(1-x)+0.019\; x(1-x)\backslash quad\; \backslash text\; \{\; for\; \}\; A\; l\_x\; G\; a\_\{1-x\}\; N$$ $$\epsilon (x)=\frac{a_{subs}-a(x)}{a(x)}\backslash varepsilon(x)=\backslash frac\{a\_\{\{subs\; \}\}-a(x)\}\{a(x)\}$$ $$\begin{array}{c}{\displaystyle a(x)=0.31986-0.00981x\text{ for }A{l}_{x}G{a}_{1-x}N}\end{array}\backslash begin\{aligned\}\; a(x)=0.31986-0.00981\; x\; \backslash quad\; \backslash text\; \{\; for\; \}\; A\; l\_x\; G\; a\_\{1-x\}\; N\; \backslash end\{aligned\}$$ $$P_{pz\mathrm{\_}GaN}=-0.918\epsilon (x)+9.541\epsilon (x{)}^{2}x=0P\_\{pz\backslash \_GaN\}=-0.918\; \backslash varepsilon(x)+9.541\; \backslash varepsilon(x)^2\; \backslash quad\; x=0$$ $$P_{pz}=x{P}_{pz\mathrm{\_}AlN}[\epsilon (x)]+(1-x)P_{p{z}_{-}GaN}[\epsilon (x)]P\_\{p\; z\}=x\; P\_\{pz\backslash \_AlN\}[\backslash varepsilon(x)]+(1-x)\; P\_\{p\; z\_\{-\}\; G\; a\; N\}[\backslash varepsilon(x)]$$ $$P_{total}=P_{sp}+P_{pz}P\_\{total\; \}=P\_\{s\; p\}+P\_\{p\; z\}$$ $$P=screening\times P_{total}P=\; screening\; \backslash times\; P\_\{total\; \}$$

2.9 碰撞电离模型 Chynoweth Model

$$\begin{array}{c}{\displaystyle {\alpha }_n={\alpha }_n^{\mathrm{\infty }}{e}^{-{\left(\frac{F_{cn}}{F}\right)}^{{\kappa }_n}}}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_n=\backslash alpha\_n^\{\backslash infty\}\; e^\{-\backslash left(\backslash frac\{F\_\{c\; n\}\}\{F\}\backslash right)^\{\backslash kappa\_n\}\}\; \backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle {\alpha }_p={\alpha }_p^{\mathrm{\infty }}{e}^{-{\left(\frac{{}_{cp}}{F}\right)}^{{\kappa }_p}}}\end{array}\backslash begin\{aligned\}\; \backslash alpha\_p=\backslash alpha\_p^\{\backslash infty\}\; e^\{-\backslash left(\backslash frac\{\{\; \}\_\{c\; p\}\}\{F\}\backslash right)^\{\backslash kappa\_p\}\}\; \backslash end\{aligned\}$$

碰撞电离参数设置

	${\alpha }^{\mathrm{\infty }}(1\mathrm{/}m)\backslash alpha^\{\backslash infty\}(1\; /\; m)$	$F_{\mathrm{c}}(V\mathrm{/}m)F\_\{\backslash mathrm\{c\}\}(V\; /\; m)$	$\kappa \backslash kappa$	Feild range to $(\mathrm{V}\mathrm{/}\mathrm{m})(\backslash mathrm\{V\}\; /\; \backslash mathrm\{m\})$
Electron	$2\times 10^{8}2\; \backslash times\; 10^\{8\}$	$3\times 10^{9}3\; \backslash times\; 10^\{9\}$	1	$3.2\times 10^{8}3.2\; \backslash times\; 10^\{8\}$
	$1\times 10^{7}1\; \backslash times\; 10^\{7\}$	$2.2\times 10^{9}2.2\; \backslash times\; 10^\{9\}$	1	$\mathrm{\infty }\backslash infty$
Hole	$1.34\times 10^{10}1.34\; \backslash times\; 10^\{10\}$	$2.03\times 10^{9}2.03\; \backslash times\; 10^\{9\}$	1	$\mathrm{\infty }\backslash infty$

三、结果与讨论

3.1 能带结构示意图

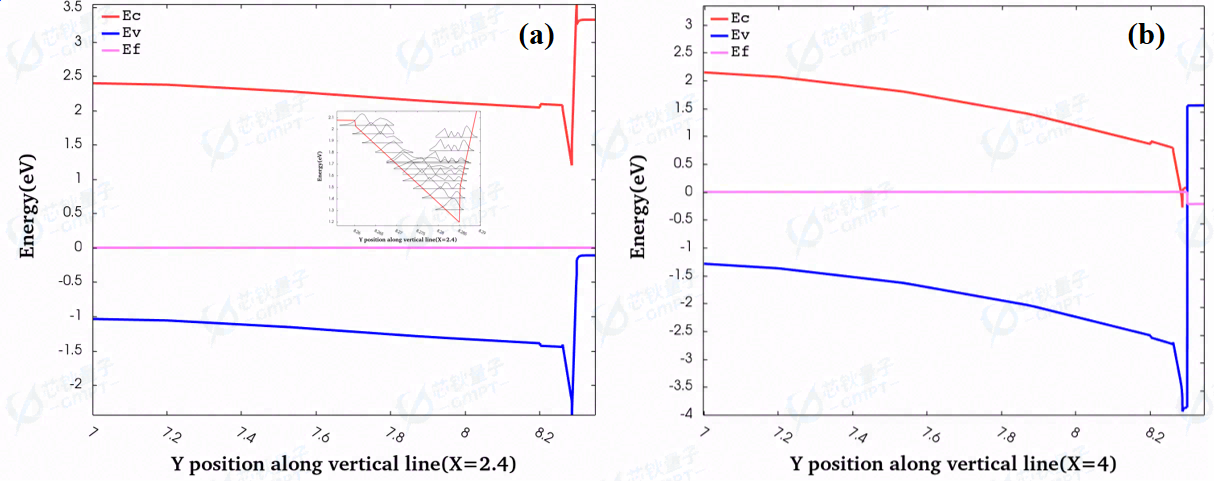
图2.（a）p-GaN/Al_0.26GaN/GaN channel界面，（b）SiN/Al_0.26GaN/GaN channel界面能带结构分布

  仿真工作同时考虑了势垒层以及反势垒层的AlGaN和沟道层GaN的极化效应，两个界面的极化正电荷使得沟道产生三角势垒阱将电子约束在沟道层中。图2（a）展示了p-GaN/Al_0.26GaN/GaN channel界面的纵向能带分布以及电子波函数的分布。由于p-GaN栅的引入提高了沟道处的电势，栅下的二维电子气被耗尽，从而实现了常断（normally-off）操作，即所设计结构为增强型器件。而在栅极以外位置，如图2（b）所示的SiN/Al_0.26GaN/GaN channel界面的纵切的能带分布，Al_0.26GaN/GaN界面产生了2DEG。

3.2 正向导通特性

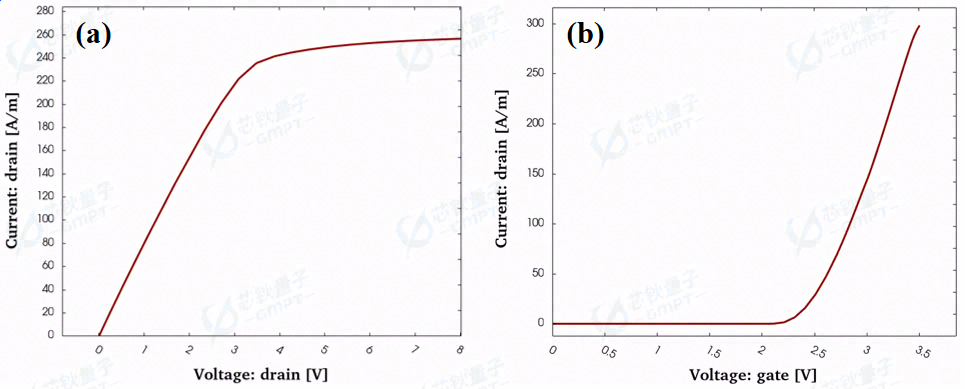
图3. （a）输出特性曲线（V_GS=3.5 V），（b）转移特性曲线（V_DS=5 V）

  图3（a）和（b）分别展示了p-GaN HEMT正向导通特性中的输出特性曲线和转移特性曲线。其中，图3（a）是在V_GS=3.5 V时，即器件沟道已经开启，漏极电压从0扫到8 V的输出特性曲线，器件实现了很好的导通特性。当V_GS=3.5 V, V_DS=8 V时，器件的输出电流能达到253 A/m。图3（b）的转移特性曲线展示了器件良好的增强型特性，即器件的阈值电压大于0 V，且达到了2.1 V（定义为漏极电流达到1mA时的栅极电压）。因此，p-GaN 栅极结构是实现常关型GaN HEMT的有效结构设计之一。

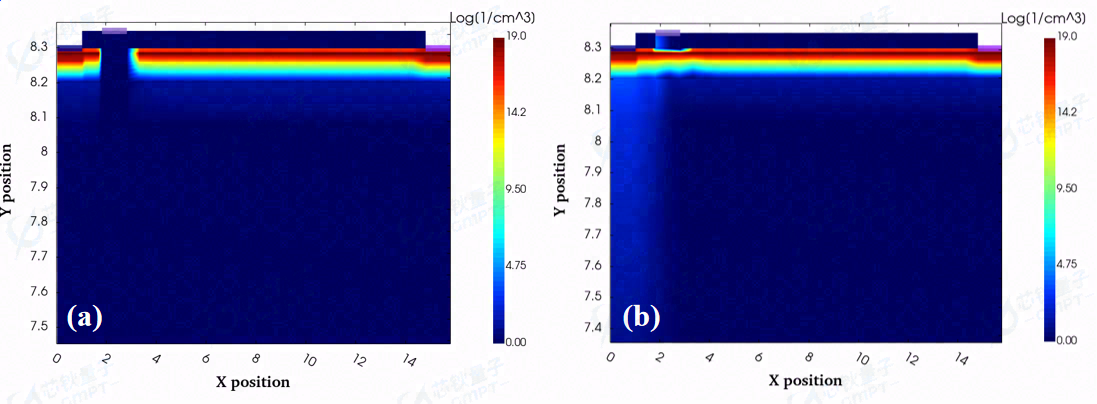
图4.（a）V_GS=0 V，（b）V_GS=3.5 V时的二维电子浓度分布（V_DS=5 V）

  图4（a）和（b）分别给出了在开启和关闭状态下器件的二维电子浓度分布图。当V_GS=0 V时，器件处于关态，栅下沟道中没有2DEG。当V_GS=3.5 V, 器件处于正常导通状态，栅下能带势垒降低，导带穿过费米能级，使得沟道中形成2DEG。

3.3 关断特性

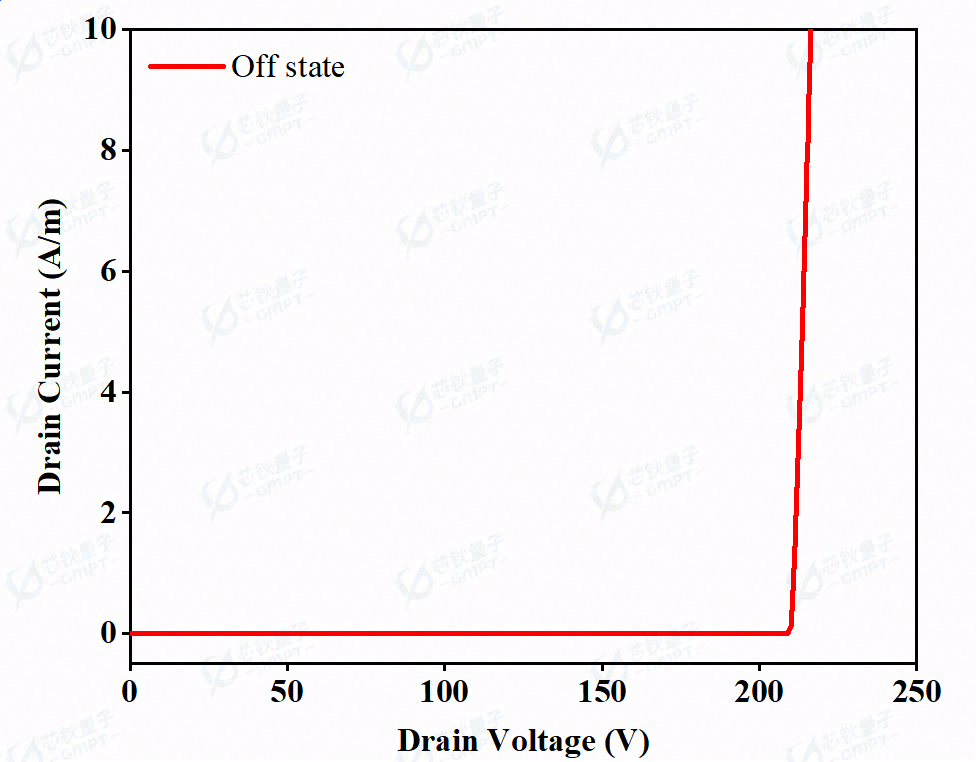
图5. 器件关态击穿曲线（V_GS=0 V）

  对于功率器件，正向导通特性和反向关断特性是两个需要折中考虑的方面。在实现提升的导通特性同时，高的关态击穿电压也是必要要求。图5展示了器件在V_GS=0 V时，漏电电压在158 V之前都保持很好的关断性能。

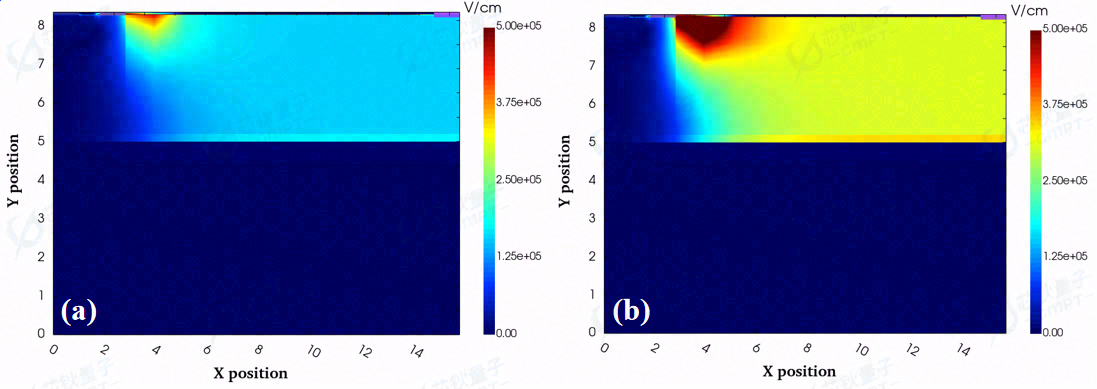
图6.关断状态下（a）V_DS=50 V，（b）V_DS=100 V二维电场分布

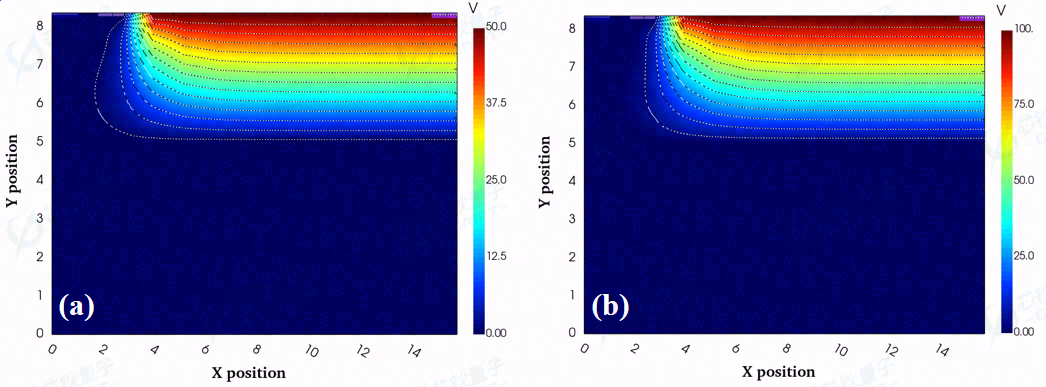
图7. 关断状态下（a）V_DS=50 V，（b）V_DS=100 V二维电势分布

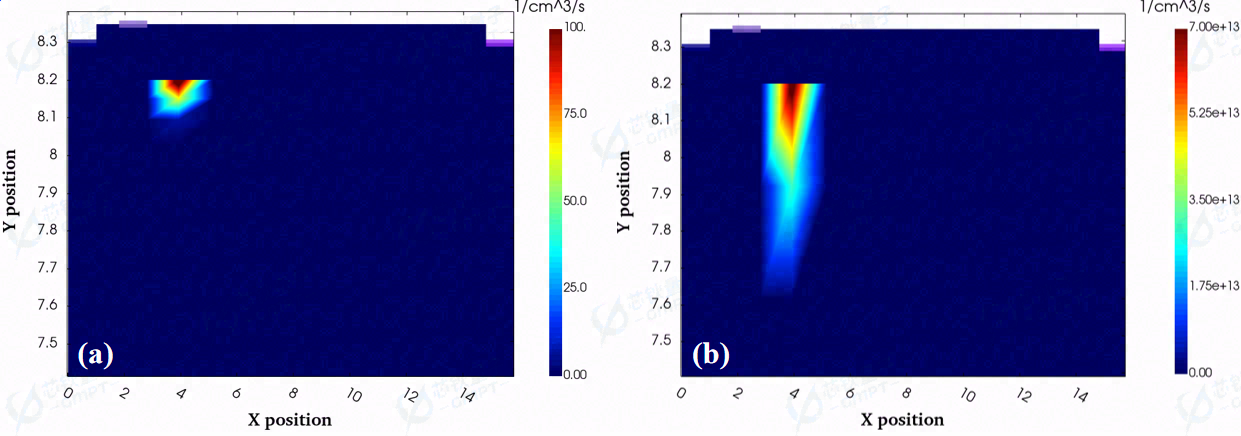
图8. 关断状态下（a）V_DS=50 V，（b）V_DS=100 V二维碰撞电离分布

  图6和图7展示了器件处于关态时，不同的漏极偏置电压下的电场分布和电势分布。随着漏极偏置电压的增大，器件的耗尽区从漏端向栅-源端拓展，且栅极靠近漏极接触边缘的电场最强。另外，图8中给出了漏极偏置电压为50 V和100 V时的二维碰撞电离率分布。该图很好地揭示了对于HEMT器件，关态时最强的碰撞电离出现在栅极靠近漏极一侧的边缘，即图7中的最强电场分布位置，这符合在仿真中所用的Chynoweth模型。因此，设计有效的边缘终端去缓解栅极边缘强电场是提升当前GaN HEMT器件耐压的关键之一。

3.4 电容-频率特性

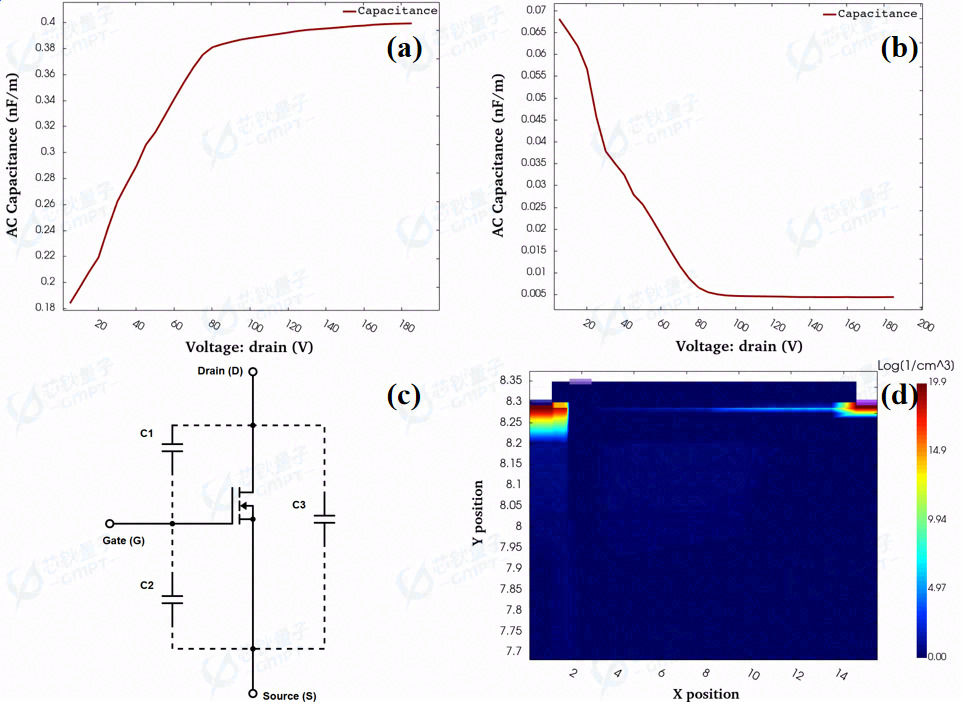
图9. （a）C_GS-V特性曲线，（b）C_GD-V特性曲线，（c）等效电路模型C1为C_GD， C2 为C_GS，（d）沟道完全耗尽时二维电子浓度分布

  在CMOS器件模型中，Meyer电容模型被广泛用于描述非零VDS时栅下电荷的非均匀分布和C_GS/C_GD比例。而p-GaN HEMT凭借其在高V_DS时，耗尽区沿栅极边缘扩展的边缘电容，以及栅极到源极和栅极到漏极的串联电阻，表现出优异的C_GD-V_DS特性^[1]。栅极电容C_G的模型可由下列公式描述。

$$\left[\begin{array}{c}{C}_{\mathrm{G}\mathrm{D}}(v_{\mathrm{D}\mathrm{S}},v_{\mathrm{G}\mathrm{S}})\\ \\ C_{\mathrm{G}\mathrm{S}}(v_{\mathrm{D}\mathrm{S}},v_{\mathrm{G}\mathrm{S}})\end{array}\right]=\left[\begin{array}{c}{C}_{\mathrm{G}\mathrm{D}0}\\ \\ C_{\mathrm{G}\mathrm{S}0}\end{array}\right]+\left[\begin{array}{c}{k}_1\left(v_{\mathrm{D}\mathrm{S}}\right)\cdot C_{\mathrm{G}-\mathrm{c}\mathrm{h}}(v_{\mathrm{G}\mathrm{S}},v_{\mathrm{G}\mathrm{D}})\\ \\ k_2\left(v_{\mathrm{D}\mathrm{S}}\right)\cdot C_{\mathrm{G}-\mathrm{c}\mathrm{h}}(v_{\mathrm{G}\mathrm{S}},v_{\mathrm{G}\mathrm{D}})\end{array}\right]\backslash left[\backslash begin\{array\}\{l\}C\_\{\backslash mathrm\{GD\}\}\backslash left(v\_\{\backslash mathrm\{DS\}\},\; v\_\{\backslash mathrm\{GS\}\}\backslash right)\; \backslash \backslash \backslash \backslash \; C\_\{\backslash mathrm\{GS\}\}\backslash left(v\_\{\backslash mathrm\{DS\}\},\; v\_\{\backslash mathrm\{GS\}\}\backslash right)\backslash end\{array\}\backslash right]=\backslash left[\backslash begin\{array\}\{l\}C\_\{\backslash mathrm\{GD\}\; 0\}\; \backslash \backslash \backslash \backslash \; C\_\{\backslash mathrm\{GS\}\; 0\}\backslash end\{array\}\backslash right]+\backslash left[\backslash begin\{array\}\{l\}k\_1\backslash left(v\_\{\backslash mathrm\{DS\}\}\backslash right)\; \backslash cdot\; C\_\{\backslash mathrm\{G\}-\backslash mathrm\{ch\}\}\backslash left(v\_\{\backslash mathrm\{GS\}\},\; v\_\{\backslash mathrm\{GD\}\}\backslash right)\; \backslash \backslash \backslash \backslash \; k\_2\backslash left(v\_\{\backslash mathrm\{DS\}\}\backslash right)\; \backslash cdot\; C\_\{\backslash mathrm\{G\}-\backslash mathrm\{ch\}\}\backslash left(v\_\{\backslash mathrm\{GS\}\},\; v\_\{\backslash mathrm\{GD\}\}\backslash right)\backslash end\{array\}\backslash right]$$

  本项工作中，在沟道关断状态下，分别计算栅极电压为0 V时的C_GS-V特性曲线和C_GD-V特性曲线，如图9（a）和图9（b）所示，其展示了当漏极偏压慢慢增大时，沟道中的载流子被耗尽，从而出现电容随着漏极电压增加而减小的现象。当漏电偏置电压大于80 V时，沟道被完全耗尽，如图9（d）所示。因此，随着漏极偏置的增大，电容几乎不变。

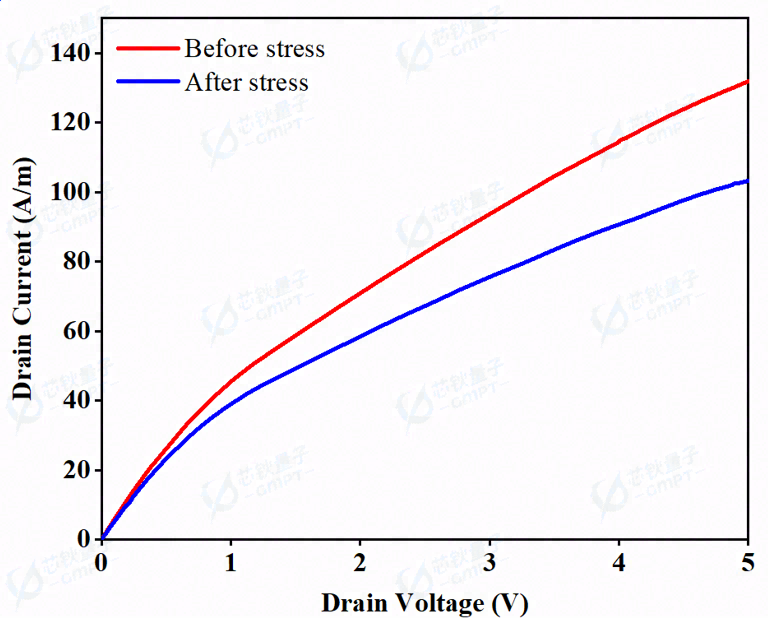
3.5 电流崩塌特性

图10. Stress过程前后的输出特性曲线（V_GS=3 V, V_GS=0-3 V）

  由于缺陷的存在，当器件处于高频运用场景时，即器件不断地快速开关过程中，GaN缓冲层和界面附近(在AlGaN层中或在AlGaN/钝化绝缘层界面上) 的缺陷会捕获沟道热电子，从而造成沟道电子浓度的下降，输出电流密度降低，即电流崩塌现象发生，如图10所示。目前已有相关改善方法，例如引入场板（field plate），利用其产生的相反方向的垂直电场分量，排斥被表面捕获的热电子^[2]。

四、总结

  本文对p-GaN HEMT器件进行了仿真和设计，介绍了仿真中引用的物理模型的公式，并展示了器件的仿真结果，包括能带结构、输出特性、转移特性、关断特性、电容-频率特性和电流崩塌特性。通过Nuwa TCAD软件得到的仿真结果，本文进一步分析了器件内部机理，包括能带分布、载流子迁移、极化效应、碰撞电离、耗尽区扩散和缺陷捕获热电子等，为p-GaN HEMT器件结构分析和器件性能提升提供了思路。

参考文献

[1] C. Sun, Z. Niu and S. Yang, "Dynamic Gate Capacitance Model for Switching Transient Analysis in P-GaN Gate HEMTs," 2023 35th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Hong Kong, 2023, pp. 135-138.

[2] I. Hwang et al., "Impact of Channel Hot Electrons on Current Collapse in AlGaN/GaN HEMTs," in IEEE Electron Device Letters, vol. 34, no. 12, pp. 1494-1496.